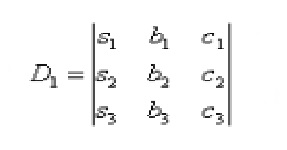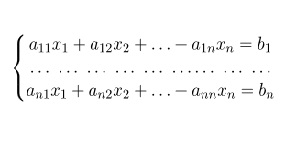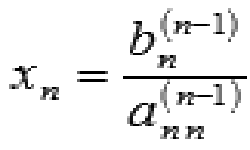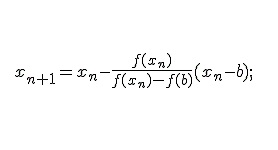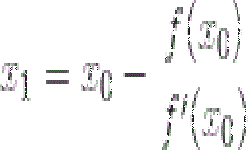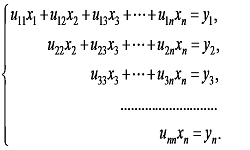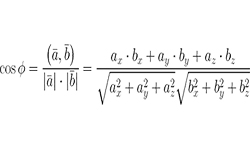Алгебра

Система линейных уравнений — это несколько уравнений линейного вида, объединенных в единую систему из n позиций. Решение системы означает нахождение одного решения, множества решений либо установления несовместимости системы. Существует довольно много методов решения СЛУ, один из них — метод Крамера. Данный метод применим, когда число неизвестных совпадает с числом уравнений. Обязательное условие — …

Решить систему линейных алгебраических уравнений, значит, найти всю совокупность чисел х1, х2, ..., хn, при подстановке которых в систему вместо неизвестных уравнения системы обращаются в тождество. Существует несколько методов решения систем уравнения, одним из них является матричный метод. Этот метод применяют, когда число неизвестных совпадает с числом уравнений в системе. …

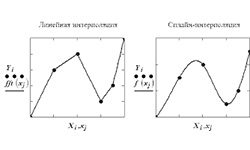
Интерполирование — это метод вычисления промежуточных значений исследуемой функции по известным значениям. Методы линейной интерполяции позволяют математически спрогнозировать производственные ситуации путем вычисления значения интерполированной координаты Y по заданному параметру координаты Х при известных координатах 2-х точек линейной функции. Пусть координаты первой точки линейной функции Х0, Y0, второй — Х1, Y1. Прямая между …

Для решения любой системы линейных уравнений метод Гаусса или метод последовательного исключения неизвестных является наиболее универсальным и достаточно простым при небольшом количестве переменных. Этот метод универсален, его применяют, когда система уравнений имеет: единственное решение; бесконечное множество решений; вовсе не имеет решений. Суть метода состоит в переходе от заданной системы линейных …

Одним из вариантов решения нелинейных уравнений является метод хорд. Такое название метод получил потому, что точка деления — это место пересечения отрезка — хорды с осью абсцисс. В отличии от метода дихотомии, здесь отрезок делится в точке, расположенной от границ отрезка пропорционально абсолютному значению функции на краях. На каждом этапе поиска функция …

Для нахождения приближенного значения корней часто применяется метод Ньютона или метод касательных. Уравнение f (х) = 0 имеет единственное решение на отрезке |аb|, если: функция у = f (х) определена и непрерывна при ; значения функции на концах отрезка |аb| разнознаковые, т.е. f (а)•f (b)< 0; в промежутке |аb| производные …

Метод LU — разложения (декомпозиции) — один из способов решения системы линейных уравнений. Алгоритмы метода схожи с алгоритмами метода Гаусса. Суть метода состоит в том, чтобы представить исходную матрицу коэффициентов А как произведение двух треугольных матриц. А = LU, где L — нижняя треугольная матрица с единичной диагональю, U — верхняя треугольная матрица. LU — …

Равенство, содержащее лишь одну переменную исключительно в первой степени, представляет собой линейное уравнение. Такое уравнение имеет вид: ах + b = 0, где а, b — коэффициенты, х -переменная. Уравнения, которые путем равносильных преобразований можно привести к виду ах + b = 0, называют уравнениями, сводящимися к линейным уравнениям. Решение линейных …

Под термином угол между векторами, отложенными от одной точки, подразумевается кратчайший угол между ними, полученный путем вращения одного из векторов вокруг своего начала до сонаправленности с другим. Величина угла между двумя векторами заключена в промежутке от 0° до 180°. Угол между двумя перпендикулярными векторами равняется 90°. Угол между нулевыми или …

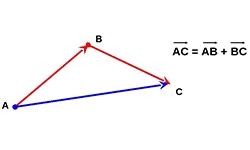
Вектором называется отрезок определенной длины с указанием стрелкой его направления в пространстве. В сложных строительных, электротехнических и других инженерных расчетах приходится выполнять такую операцию, как сложение векторов. Сумму векторов можно найти способом геометрического сложения. 1. При геометрическом сложении один из расположенных в двухмерном или трехмерном пространстве векторов путем параллельного смещения …