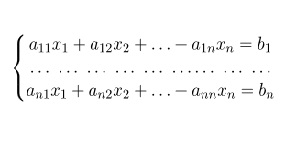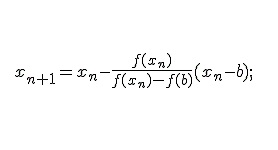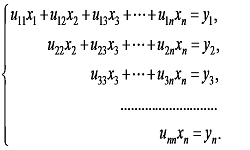Решение нелинейных уравнений методом Ньютона

Для нахождения приближенного значения корней часто применяется метод Ньютона или метод касательных.

Уравнение f (х) = 0 имеет единственное решение на отрезке |аb|, если:

• функция у = f (х) определена и непрерывна при ;
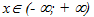• значения функции на концах отрезка |аb| разнознаковые, т.е. f (а)•f (b)< 0;
• в промежутке |аb| производные f'(x) и f''(x) сохраняют постоянный знак, т.е. функция монотонна и выпукла вверх или вниз;
• производная .

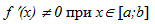Суть метода в том, что на отрезке |аb| берется число х0 при котором f (х0) и производная f '(х) имеют один и тот же знак, т.е. f (x0) • f'' (x) > 0.

В этой точке касательная к кривой у = f (x) выражена уравнением:

Пусть у = 0, тогда х1 — точка пересечения касательной с осью Ох будет равна:
Таким же образом находим точку х2, х3 и т.д.

Уравнение касательной к функции f (х), проведенной в точке хn, будет иметь вид:
Вычисления заканчиваются, если достигнуто условие: | f (хn) / f' (xn) | < е,
где е — заданная точность. Это называется сходимостью метода.

Метод Ньютона имеет квадратичную сходимость.