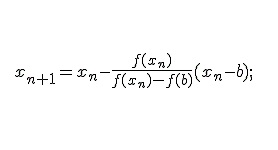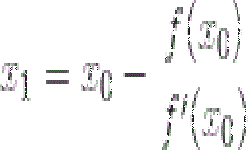Решение линейного уравнения

Равенство, содержащее лишь одну переменную исключительно в первой степени, представляет собой линейное уравнение. Такое уравнение имеет вид: ах + b = 0, где а, b — коэффициенты, х -переменная.

Уравнения, которые путем равносильных преобразований можно привести к виду ах + b = 0, называют уравнениями, сводящимися к линейным уравнениям.

Решение линейных уравнений подразумевает определение наличия или отсутствия его корней.

Алгоритм решения:

• если есть скобки, раскрываем их;
• слагаемые, содержащие «х», переносим в одну часть от знака равенства, без «х» — в другую часть. При переносе из одной части уравнения в другую знак меняем на противоположный;
• приводим подобные слагаемые;
• обе части уравнения делим на число а, не равное 0.

1. Если число а отлично от 0: перенесем в уравнении ах + b = 0 свободный член b в другую часть равенства, изменив знак на противоположный: ах = — b.
   Разделив обе части на коэффициент а (а не равно 0), найдем искомый корень уравнения: х = — b/а.
2. Если а равно 0, а свободный член b не равен нулю, получим уравнение: 0х = — b, которое не имеет решения, т.к. при умножении числа на 0 получается 0, а в нашем случае b не равно 0.
3. Если коэффициенты а, b равны 0, корнем уравнения является любое число, т.к. при подстановке в уравнение вместо х любого числа получается верное равенство 0 = 0.

С помощью онлайн калькулятора вы можете быстро найти корни уравнения. Вам нужно лишь ввести значения коэффициентов а, b и нажать кнопку Решить.