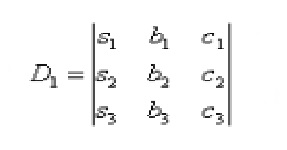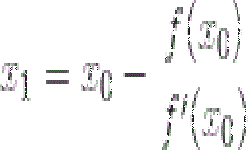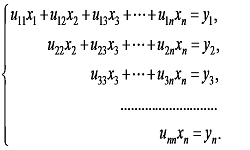Решить систему уравнений методом обратной матрицы

Решить систему линейных алгебраических уравнений, значит, найти всю совокупность чисел х₁, х₂, ..., х_n, при подстановке которых в систему вместо неизвестных уравнения системы обращаются в тождество.

Существует несколько методов решения систем уравнения, одним из них является матричный метод. Этот метод применяют, когда число неизвестных совпадает с числом уравнений в системе.

Чтобы решить СЛАУ матричным методом, необходимо:

1. Найти определитель матрицы А. Если определитель равняется 0, решить систему методом обратной матрицы нельзя (решается методом Гаусса).
2. Если определитель не равен 0, находим обратную матрицу А-1 через алгебраические дополнения.
3. Умножаем обратную матрицу на вектор результата В, получаем вектор результата
Х = ({x₁, x₂, ..., x_n}, т.е Х = А-1•В

Пусть задана система n линейных уравнений с n неизвестными: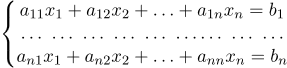

1. Матричный вид уравнения: А х Х = В, где основная матрица системы
матрица-столбец неизвестных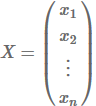
матрица свободных членов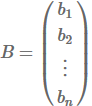
2. Обе части уравнения умножаем на А-1 (слева)
А-1 • (А • Х) = А-1 • В

Т.к. А-1 • А = Е, где Е — единичная матрица порядка n на n, тогда Е • Х = А-1 • В

Отсюда, Х = А-1 • В.

3. Находим обратную матрицу А-1.

4. Решение СЛАУ находим по формуле: Х = А-1 • В (обратную матрицу А-1 умножаем на столбец свободных членов В).

Задачу решения СЛАУ матричным способом можно быстро решить с помощью представленного на сайте онлайн калькулятора.