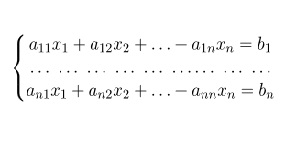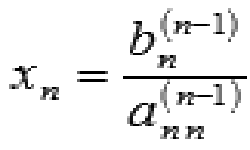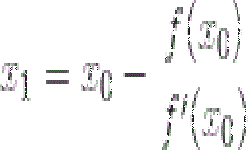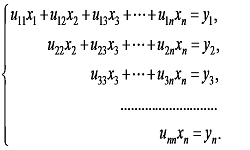Решение системы линейных уравнений методом Крамера

Система линейных уравнений — это несколько уравнений линейного вида, объединенных в единую систему из n позиций. Решение системы означает нахождение одного решения, множества решений либо установления несовместимости системы. Существует довольно много методов решения СЛУ, один из них — метод Крамера. Данный метод применим, когда число неизвестных совпадает с числом уравнений. Обязательное условие — главный определитель системы не должен равняться 0.

Пусть дана система 3-х уравнений с 3-мя неизвестными:
а₁х₁ + b₁х₂ + с₁х₃ = s₁
а₂х₁ + b₂х₂ + с₂х₃ = s₂
а₃х₁ + b₃х₂ + с₃х₃ = s₃

Чтобы решить систему, необходимо найти определитель основной матрицы системы (D):

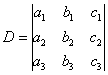
При D = 0 у системы нет решений либо их бесконечное множество.
При D не равном 0 система имеет единственное решение, которое можно вычислить методом Крамера.

Для дальнейшего решения системы найдем еще три определителя матриц, полученных из основной матрицы:

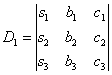
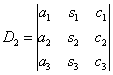
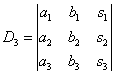
Определяем неизвестные х₁, х₂, х₃ по формулам: х₁ = D₁ / D, х₂ = D₂ / D, х₃ = D₃ / D.

Если уравнения исходной системы при подстановке в них значений х₁, х₂, х₃ обращаются в тождества, значит, система решена верно.