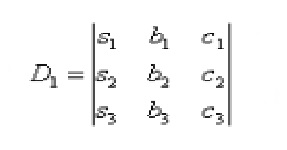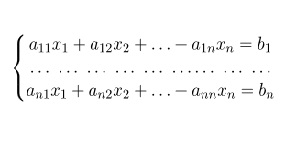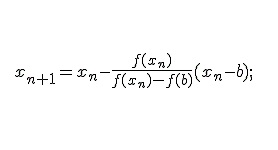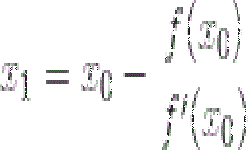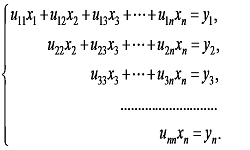Решение системы линейных уравнений методом Гаусса

Для решения любой системы линейных уравнений метод Гаусса или метод последовательного исключения неизвестных является наиболее универсальным и достаточно простым при небольшом количестве переменных. Этот метод универсален, его применяют, когда система уравнений имеет:

• единственное решение;
• бесконечное множество решений;
• вовсе не имеет решений.

Суть метода состоит в переходе от заданной системы линейных уравнений к более простой с помощью таких эквивалентных преобразований в системе, как:

• перемена двух уравнений местами;
• умножение обеих частей уравнения на любое действительное число, не равное 0;
• прибавление к одному уравнению соответствующих частей другого, умноженных на произвольное число.

С помощью преобразований последовательно исключаем одну переменную за другой пока в одной из строк не будет определена переменная x_i.

Метод Гаусса позволяет решать СЛАУ при небольшом числе вычислительных операций.

Алгоритм решения:

• записываем систему в виде расширенной матрицы;
• прямой ход — приводим матрицу к ступенчатому виду;
• обратный ход — приводим матрицу к специальному ступенчатому виду.

Пусть дана система из n уравнений с n неизвестными переменными:

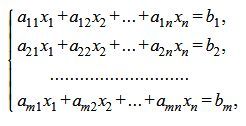
Определитель основной матрицы не равен 0.

Исключим из всех уравнений системы переменную х₁, начиная со 2-го, для чего:

• ко 2-му уравнению прибавим 1-е, умноженное на — а₂₁/а₁₁;
• к 3-му уравнению прибавим 1-е, умноженное на — а₃₁/а₁₁, и т.д.;
• к n-му уравнению прибавим 1-е, умноженное на — а_n1/а₁₁.

В результате преобразований система приняла вид:

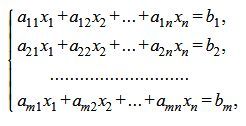
Далее таким же путем исключаем неизвестную переменную х₂ из всех уравнений, начиная с 3-го.

Для этого к 3-му уравнению прибавляем 2-е, умноженное на — а₃₂/а₂₂ и т.д. К n-му уравнению прибавим 2-е, умноженное на — а_n2/а₂₂.

Таким же способом исключаем неизвестную х₃ из всех уравнений системы, начиная с 4-го.

Прямой ход продолжается, пока в последнем уравнении не останется единственная неизвестная. Система будет иметь вид:

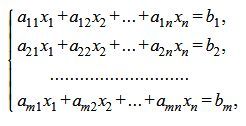
а_nn^(n-1) х_n = b_n^(n-1)

После окончания прямого хода метода Гаусса — последовательного исключения неизвестных, вычисляем неизвестную в последнем уравнении:

• из последнего уравнения системы находим х_n по формуле:
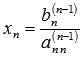
• из предпоследнего уравнения находим х^n-1 и т.д.
• из первого уравнения находим х₁.

Последовательное нахождение неизвестных, начиная с последнего уравнения к первому, называется обратным ходом.

Заметим, если в матрице есть хоть одна нулевая строка, у которой правая часть (свободный член) не равна 0, система несовместима, решения отсутствуют.

Для быстрого и правильного решения СЛАУ методом Гаусса можно воспользоваться калькулятором онлайн.