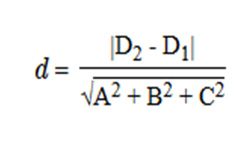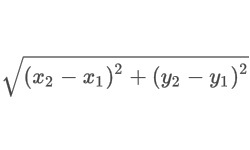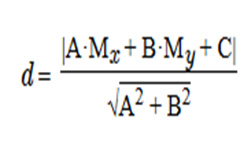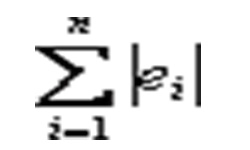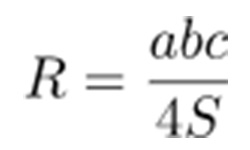В строительной сфере, машиностроении, самолетостроении и многих других отраслях очень важно уже в начальной стадии проектирования точно рассчитать расстояние между точками, от точки до прямой и т.д. Возьмем прямую L и точку М, не принадлежащую заданной прямой. Проведем через точку М прямую, перпендикулярно к прямой L. Величина перпендикуляра, опущенного от точки М до прямой L на плоскости, будет наименьшим из всех возможных расстоянием между точкой и прямой.
Пусть прямая L на плоскости задана уравнением Ax + By + C = 0. Расстояние d от точки М с координатами (Мх,Му) в декартовой системе до прямой L вычисляем по формуле: 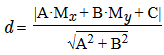
В том случае, когда известны координаты точки на плоскости М1 (х1,у1) и координаты точки Н1 (х2,у2) — точки пересечения перпендикуляра, проведенного от точки М1 к прямой, расстояние между М1 и прямой можно рассчитать по их координатам: ![]()
Воспользовавшись онлайн калькулятором вы сможете быстро и правильно рассчитать расстояние между точкой и прямой.