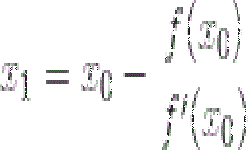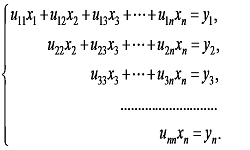Одним из вариантов решения нелинейных уравнений является метод хорд. Такое название метод получил потому, что точка деления — это место пересечения отрезка — хорды с осью абсцисс. В отличии от метода дихотомии, здесь отрезок делится в точке, расположенной от границ отрезка пропорционально абсолютному значению функции на краях.
На каждом этапе поиска функция f (х) заменяется хордой, которая пересекаясь с осью Х дает приближение корня. Хорды проходят через края отрезков, где f (х) имеет противоположные знаки.
Семейство хорд можно строить при фиксировании одного из концов отрезка:
- при неподвижном левом конце хорд;
- при неподвижном правом конце хорд.
В первом случае: 
, где|аb| — интервал, z = а, начальная точка х0 = b.
Во втором случае: 
, где z = b, начальная точка х0 = а.
Поиск хордой заканчивается при условии: 
.
Метод хорд решения нелинейных уравнений f (x)=0
| Введите интервал |
a = | b = |
Введите левую часть уравнения (неизвестная — x):
