Вектором называется отрезок определенной длины с указанием стрелкой его направления в пространстве. В сложных строительных, электротехнических и других инженерных расчетах приходится выполнять такую операцию, как сложение векторов.
Сумму векторов можно найти способом геометрического сложения.
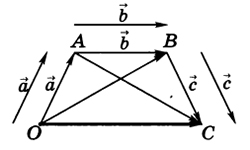
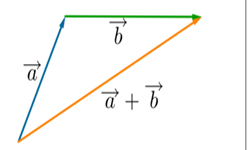
1. При геометрическом сложении один из расположенных в двухмерном или трехмерном пространстве векторов путем параллельного смещения переносится своим началом в конец другого вектора. Суммарным вектором будет вектор, начало которого совпадает с началом 1-го вектора, а конец — с концом 2-го. Сложение векторов производится по правилу треугольника или параллелограмма. При сложении векторов по правилу параллелограмма оба вектора откладываются от одной точки, затем достраивается параллелограмм, стороны которого параллельны заданным векторам. Суммарным вектором является диагональ параллелограмма, идущая от общего начала исходных векторов к противоположной вершине.
2.Рассчитать сумму векторов можно с помощью системы уравнений.
Суммой векторов а и b является вектор с, каждый элемент которого равняется попарной сумме соответствующих элементов векторов а и b.
Для двухмерного пространства сумму векторов с координатами a = {ax ; ay} и b = {bx ; by} вычисляем по формуле:
a + b = {ax + bx; ay + by}
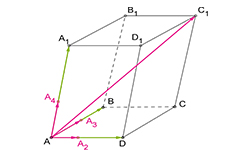
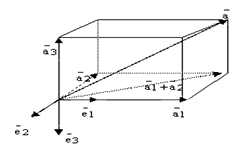
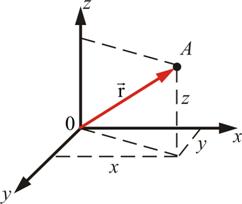
Для трехмерного пространства сумму векторов, имеющих координаты a = {ax ; ay ; az} и b = {bx ; by ; bz} находим по формуле:
a + b = {ax + bx; ay + by; az + bz}
Для n-мерного пространства сумму вектора a = {a1 ; a2 ; ... ; an} и вектора b = {b1 ; b2 ; ... ; bn} определяем таким же способом:
a + b = {a1 + b1; a2 + b2; ... ; an + bn}
Сумма противоположных векторов a и (- а) равняется 0.
С помощью онлайн калькулятора можно легко получить уравнение, представляющее сумму заданных векторов. Для этого необходимо ввести заданные координаты каждого из векторов, расположенных в трехмерном пространстве (либо два исходных значения каждого из векторов в двухмерном пространстве) и нажать кнопку Рассчитать.