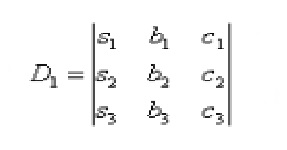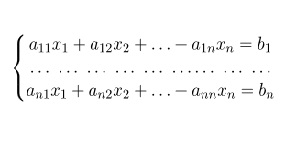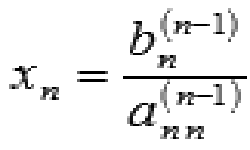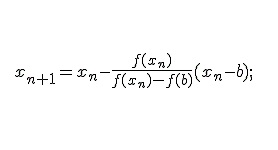Решение СЛАУ методом LU-разложения

Метод LU — разложения (декомпозиции) — один из способов решения системы линейных уравнений. Алгоритмы метода схожи с алгоритмами метода Гаусса.

Суть метода состоит в том, чтобы представить исходную матрицу коэффициентов А как произведение двух треугольных матриц.

А = LU, где L — нижняя треугольная матрица с единичной диагональю, U — верхняя треугольная матрица. LU — разложение возможно, когда:
— матрица А обратима;
— главные миноры матрицы отличны от 0.

LU — разложение используют для решения систем линейных уравнений вида: Ах = b.

Т.к. А = LU, исходную систему можно представить в виде равенства: LUх = b. Если ввести вектор у = (у₁, у₂,...,у_n)^t, равенство можно представить как систему: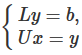
Т.е. решение системы Ах = b заключается в решении двух систем с треугольными матрицами: Lу = b, Uх = у.

На первом этапе решается система Lу = b. Т.к. L — нижняя треугольная матрица, система решается прямой подстановкой.

Запишем первую систему в виде: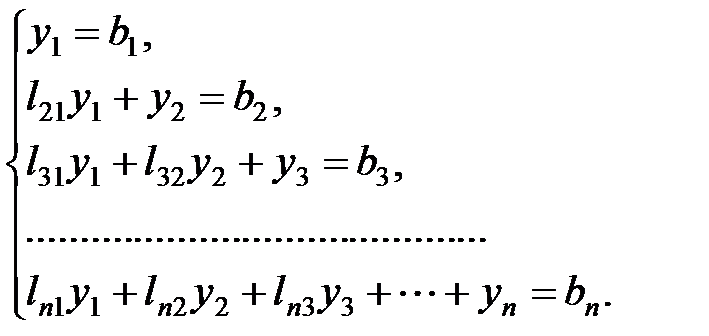
В первом уравнении вычисляем у₁, во втором — у₂, в третьем — у₃ и т.д.

Общая формула: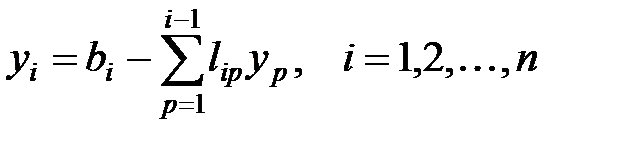
На втором этапе решается вторая система Uх = у способом обратной подстановки.
Система имеет вид: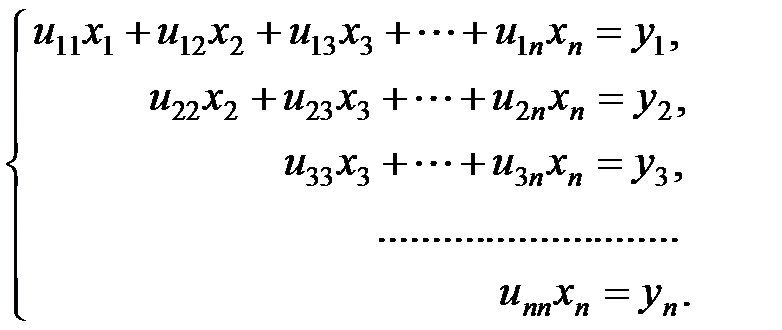
Из последнего уравнения системы находим х_n, из предпоследнего х_n-1 и т.д., из первого находим х₁.
Общая формула для решения системы имеет вид: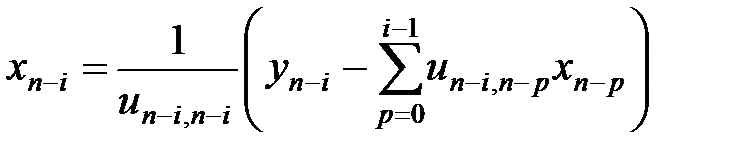
Быстро решать системы линейных уравнений методом LU — разложения можно с помощью онлайн калькулятора.