Помощник в обучении Сайт помощник в обучении. Онлайн калькуляторы, тренажеры и справочники для решения и выполнения математических и других видов задач
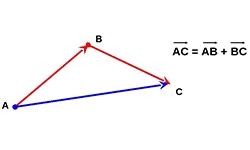
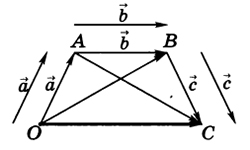
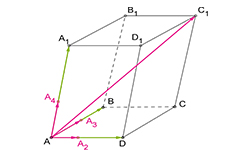
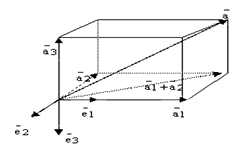
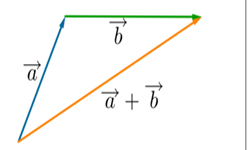
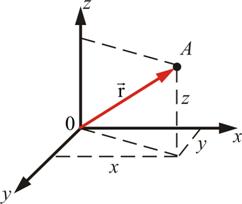
Под термином угол между векторами, отложенными от одной точки, подразумевается кратчайший угол между ними, полученный путем вращения одного из векторов вокруг своего начала до сонаправленности с другим. Величина угла между двумя векторами заключена в промежутке от 0° до 180°. Угол между двумя перпендикулярными векторами равняется 90°. Угол между нулевыми или сонаправленными векторами равняется 0°. Два противоположно направленных вектора образуют угол в 180°. Векторы образуют также острые и тупые углы.
Косинус угла между векторами (cos а) равняется отношению скалярного произведения векторов a и b на произведение модулей векторов |a| и |b|.
| cos α = | a·b |
| |a|·|b| |
Скалярное произведение рассчитывается как сумма произведений соответствующих координат. Модуль вектора равен корню квадратному из суммы квадратов координат вектора.
Если векторы заданы координатами а = {а1 ; а2 ; а3} и b = {b1 ; b2 ; b3}, скалярное произведение находим по формуле:
a × b = а1×b1 + а2×b2 + а3×b3
Косинус угла между двумя векторами в координатной форме определяем по формуле:
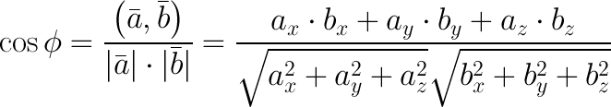Благодаря онлайн калькулятору вы можете легко определить величину угла между векторами в двухмерном и трехмерном пространстве как в градусах, так и в радианах. Вам потребуется лишь ввести координаты исходных векторов.
