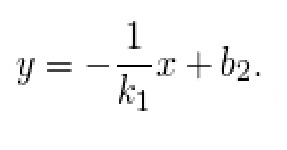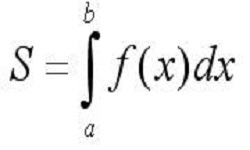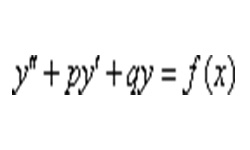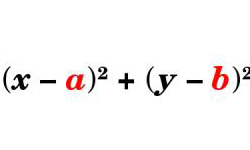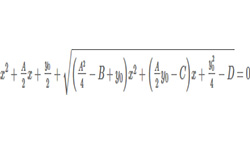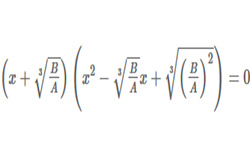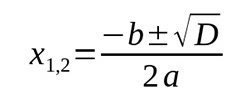Математический анализ
Расположенные на плоскости прямые (а) и (b), называются перпендикулярными, если при пересечении образуют четыре
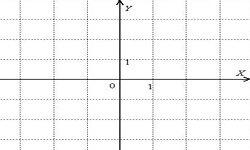
Линейными неравенствами с одной переменной х называются неравенства, в которых неизвестное находится исключительно в
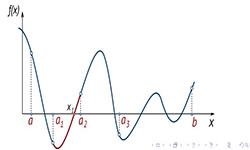
Интегрирование или решение интегралов — операция, обратная дифференцированию. Геометрический смысл интеграла для функции у =
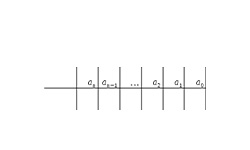
Уравнение вида: a•xn + b•xn-1 + c•x2 + d•x + e = 0 называется
Уравнение вида f (x) = 0, где f (x) — некая нелинейная функция, называется нелинейным.
В дифференциальных уравнениях (ДУ) второго порядка обязательно есть вторая производная у'', но отсутствуют производные
Окружность — геометрическое место расположения множества точек, каждая из которых равноудалена от центра окружности. Отрезок,
Равенство, содержащее неизвестное число, которое обозначено буквой, называется уравнением. Решение уравнения предполагает нахождение всех
Уравнение представляет собой равенство, содержащее букву, значение которой нужно найти. Для обозначение неизвестных чисел
Чтобы решить квадратное уравнение а2 + bх + с = 0, нужно вычислить дискриминант