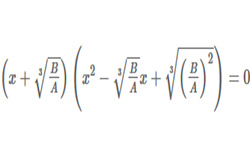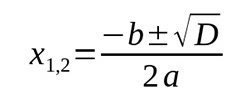В дифференциальных уравнениях (ДУ) второго порядка обязательно есть вторая производная у'', но отсутствуют производные высших порядков.
Различают два типа линейных дифференциальных уравнений (ДУ) 2-го порядка с постоянными коэффициентами: однородные и неоднородные.
Однородное ДУ имеет вид: у'' + ру' + qу = 0. В правой части уравнения всегда будет 0, р, q — числа.
Неоднородное ДУ имеет следующий вид: у'' + ру' + qу = f (х), где р, q — постоянные числа, в правой части уравнения — функция f (х), которая зависит только от х. Наиболее простой случай — f (х) является числом, кроме 0.
Решить дифференциальное уравнение, значит, найти все решения, удовлетворяющие этому уравнению.
Чтобы решить однородное уравнение 2-го порядка, нужно вначале составить характеристическое уравнение. Для этого заменим первую производную «лямбдой», а вместо у ничего не запишем. В результате получим обычное квадратное уравнение вида: λ2 + рλ + q = 0.
Далее находим корни уравнения. Здесь возможны 3 варианта.
1 вариант. Дискриминант (D) больше 0, тогда характеристическое уравнение λ2 + рλ + q = 0 имеет 2 разных действительных корня (λ1, λ2).
Общее решение ДУ принимает следующий вид: у = С1еλ1х + С2еλ2х (С1, С2 — произвольные числа).
При λ1 = 0 общее решение уравнения упрощается: у = С1 + С2еλ2х.
2 вариант. Дискриминант равен 0, тогда характеристическое уравнение имеет 2 равных действительных корня. В этом случае общее решение однородного уравнения имеет вид: у = С1еλ1х + С2хееλ1х. Т.к λ1 = λ2, в формулу можно поставить λ2.
Если оба корня равны 0, получим общее решение уравнения: у = С1е0х + С2xе0х = С1 + С2x.
3 вариант. Дискриминант меньше 0, уравнение λ2 + рλ + q = 0 имеет сопряженные комплексные корни: λ1 = а — bi, λ2 = а + bi.
Общее решение уравнения будет иметь такой вид: у = еах • (С1соs Вх + С2sinВх).
Чтобы решить неоднородное уравнение у'' + ру' + qу = f (х), нужно:
1. записать соответствующее однородное уравнение, обнулив правую часть неоднородного уравнения: у'' + ру' + qу = 0 и найти его общее решение.
2. способом подбора найти частное решение неоднородного уравнения.
3. составить общее решение неоднородного уравнения.