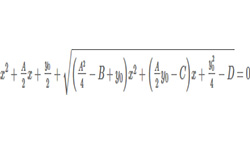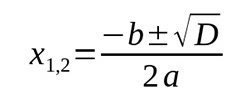Уравнение представляет собой равенство, содержащее букву, значение которой нужно найти. Для обозначение неизвестных чисел наиболее часто пользуются буквами х, у, z. Кубическое уравнение — уравнение 3-го порядка вида: ax3 + bx2 + cx + d = 0, где a не равно 0.
Решить уравнение означает найти такие значения числа х, подстановка которых в уравнение дает верное равенство. Число х будет корнем уравнения.
В кубическом уравнении 3 корня, которые могут быть как вещественными, так и комплексными. Как минимум один из них является действительным корнем.
Простейшим случаем таких уравнений является двучленное кубическое уравнение вида Ах3 + В = 0. Для решения такого уравнения необходимо:
1. разделить уравнение на коэффициент А, не равный 0, получим: х3 + В/А = 0
2. применить формулу сокращенного умножения суммы кубов, получим: 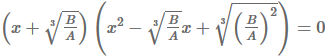 .
.
В первой скобке получим корень х, равный: ![]() .
.
Во второй скобке получим квадратный трехчлен с комплексными корнями: ![]() .
.
Уравнение вида Ах3 + Вх2 + Вх + А = 0 называется возвратным кубическим уравнением, А и В — коэффициенты.
Для решения возвратного уравнения нужно произвести группировку, после чего получим: 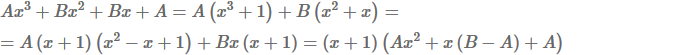
В первой скобке получим корень, равный -1. Во второй скобке у нас квадратный трехчлен Ах2 + х (В — А) + А. Для решения квадратного трехчлена определяем дискриминант, а затем находим его корни.
Кубические уравнения с рациональными корнями
Пусть х, равное 0, будет корнем уравнения Ах3 + Вх2 + Сх + D = 0, тогда свободный член D будет равен 0, а уравнение примет вид: Ах3 + Вх2 + Сх = 0.
Выносим х за скобки, получаем уравнение: х (Ах2 + Вх + С) = 0. Корни полученного квадратного трехчлена находим через дискриминант.
Найти корни кубического уравнения можно по формуле Кардано
Пусть дано уравнение А0х3 + А1х2 + А2х + А3 = 0.
Разделим все коэффициенты на А0, получим: В1 = А1 / А0, В2 = А2 / А0, В3 = А3 / А0, затем находим значение р и q: ![]() .
.
Полученные значения р и q подставляем в формулу Кардано: ![]() .
.
Выбираем значение кубических корней, чтобы их произведение равнялось — р / 3. Корни исходного уравнения будут равняться: х = у — В1 / 3.
Быстро найти корни кубического уравнения вы можете при помощи онлайн калькулятора.