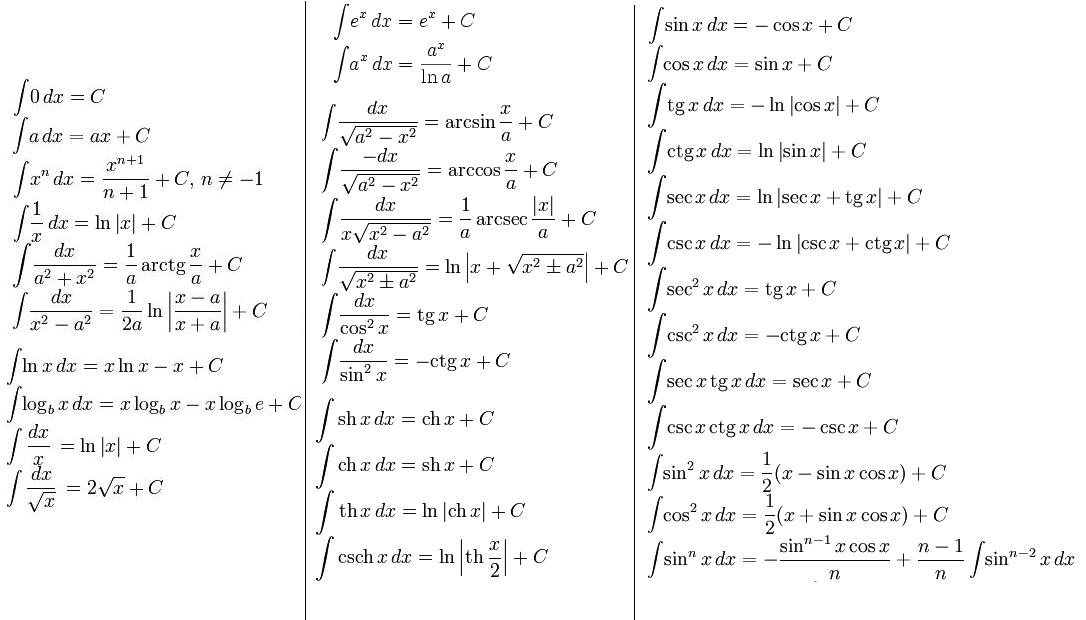Интегрирование или решение интегралов — операция, обратная дифференцированию. Геометрический смысл интеграла для функции у = f (х) — это площадь криволинейной трапеции.
Решение определенного интеграла предполагает поиск значения функции в заданных пределах.
Если интеграл неопределенный (нет границ интегрирования), решение предполагает нахождение первообразной: ![]()
ʃ – значок интеграла;
dх — значок дифференциала;
f (х) — подынтегральная функция;
f (х) dх — подынтегральное выражение;
F (х) — первообразная функция;
С — константа, которая плюсуется к ответу в любом неопределенном интеграле.
Решение интеграла означает нахождение определенной функции F (х) + C.
Если продифференцировать первообразную, мы должны получить исходное подынтегральное выражение.
Чтобы решить неопределенный интеграл, нужно превратить его в определенную функцию F (х) + C, используя таблицу.
Если интеграл табличного вида, значит он уже решен. В противном случае, интеграл нужно привести к одному из табличных интегралов, применяя основные свойства, правила и приемы решения.
Свойства интегралов:
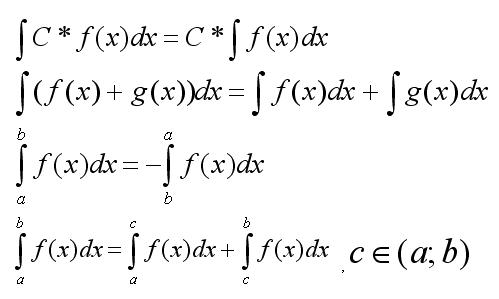
Существуют функции, интеграл от которых нельзя выразить через элементарные функции. Решаются интегралы от таких функций с помощью таких приемов, как
- — замена подынтегральной функции близкой к ней функцией, интеграл от которой можно выразить через элементарные функции;
- — интегрирование по частям по формуле:
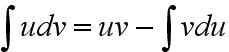
Для решения интегралов от дробно-рациональных функций, дробь раскладывают на простейшие, выделяют полный квадрат, после чего в числителе создают дифференциал знаменателя.
Чтобы решить интеграл от дробно-иррациональных функций, необходимо в подкоренном выражении выделить полный квадрат, после чего в числителе создать дифференциал подкоренного выражения.
Калькулятор решения интегралов поможет вам справиться с любыми задачами. Вам нужно:
- ввести в ячейку калькулятора подынтегральное выражение;
- ввести верхний предел для интеграла;
- ввести нижний предел для интеграла.
| При вводе функции используйте следующие обозначения: | |||
| + | сложение; | Math.log (x) | натуральный логарифм; |
| — | вычитание; | Math.cos (x) | косинус; |
| * | умножение; | Math.sin (x) | синус; |
| / | деление; | Math.exp (x) | экспонента; |
| Math.sqrt (x) | квадратный корень; | Math.pow (x,n) | возведение x в степень n; |
Пример: x^4*cos (x^2+x+1) соответствует Math.pow (x,4)*Math.cos (Math.pow (x,2)+x+1)