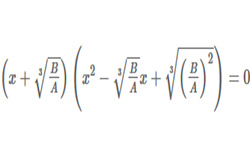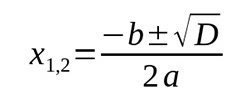Уравнение вида: a•xn + b•xn-1 + c•x2 + d•x + e = 0 называется полиномиальным уравнением n-й степени.
Квадратное уравнение вида ах2 + bx + c = 0 представляет собой простейшее полиномиальное уравнение 2-й степени.
Чтобы решить это уравнение, необходимо вычислить его корни по формуле: x = (- b ± v (b2 — 4 * a * c)) / 2 * a, где а, b — коэффициенты при х, с — константа.
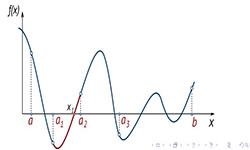
Если для уравнений 2-й, 3-й, 4-й степени существуют формулы, которые позволяют определять корни уравнения по коэффициентам, то уравнение степени выше 4-й в радикалах решить нельзя. Правда, иногда многочлен уравнения высшей степени можно разложить на множители и представить его как произведение многочленов степени не выше 4-й. Преобразованное уравнение решить будет просто.
Часто приходится решать уравнения высших степеней с целыми коэффициентами.
Пусть дано уравнение вида аnхn + аn-1хn-1 + ... +а1х +а0 = 0.
Если обе части уравнения умножить на (аn)n-1 и произвести замену у = аnх, то получим приведенное уравнение той же (n-ой) степени, которое и следует решать: хn + аn-1хn-1 + ... +а1х +а0 = 0.
Корни уравнения n-й степени с заданной точностью вычисляют путем использования численных методов. При решении уравнений нужно указать требуемую точность определения корней и число предполагаемых итераций.
Решить полиномиальное уравнение до 10 степени можно с помощью онлайн калькулятора, который быстро и правильно вычислит все корни на заданном промежутке. Для этого вам нужно ввести исходные данные в полиноминальное уравнение и задать промежуток.