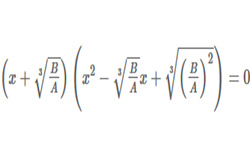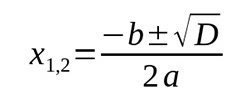Уравнение вида f (x) = 0, где f (x) — некая нелинейная функция, называется нелинейным. Виды таких уравнений: алгебраические, где функция алгебраическая, и трансцендентные, в которых функция может быть тригонометрическая, показательная и т.д.
При решении нелинейных уравнений используются прямые (точные) и итерационные (численные) методы. Решить точным методом — значит, представить решение в виде формулы, по которой находят корни уравнения. Для уравнений выше 4-й степени невозможно написать аналитическое решение.
Бывает, что в уравнении присутствуют приближенные коэффициенты. В этом случае для решения уравнения применяют итерационные методы, где заранее задается точность. Решение уравнения такими методами предполагает нахождение корней (или их отсутствие) и определение их значения с заданной точностью.
Решение нелинейных уравнений
Корнем уравнения f (x) = 0 является такое значение с, при котором f© = 0.
Уравнение f (x) = 0 имеет одно решение на отрезке |а;b| при условии, что функция f (x):
— непрерывна и монотонна на данном отрезке;
— значения функции на концах отрезка с разными знаками, т.е. f (а)• f (b) меньше 0.
Вычисление корня уравнения f (x) = 0 путем использования численных методов:
— устанавливаем знаки функции в предельных точках области ее существования
х = а, х = b;
— определяем приближенное значение корня или промежутка, в котором он находится;
— уточняем приближенное значение до определенной точности.
Данный калькулятор станет для вас надежным помощником при решении нелинейных уравнений онлайн. Вам потребуется лишь ввести исходные данные в окна калькулятора.