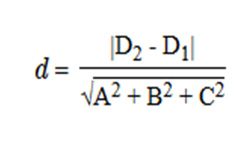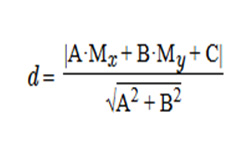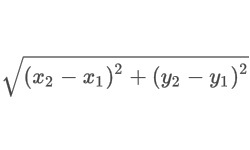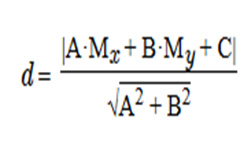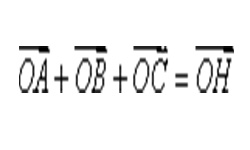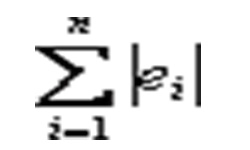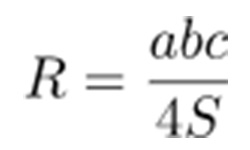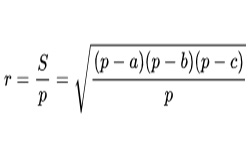Геометрия

Расстояние между параллельными плоскостями равняется величине перпендикуляра, проведенного из точки, принадлежащей одной плоскости, на

В строительной сфере, машиностроении, самолетостроении и многих других отраслях очень важно уже в начальной

Точка — одна из простейших геометрических фигур. На практике очень часто приходится определять расстояние между

При проектировании металлических, строительных и других конструкций важно уметь правильно и максимально точно вычислять

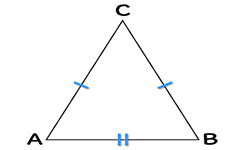
Перпендикуляр, проведенный из любой вершины треугольника на противолежащую ей сторону, будет его высотой, а

Одним из математических методов, используемых при решении определенных практических задач, является метод наименьших квадратов

Если треугольник вписан в окружность так, что его вершины располагаются на окружности, такая окружность

Треугольник — наиболее распространенная форма деталей в сферах машиностроения и строительства. Точка пересечения 3-х медиан

Окружность считается вписанной в треугольник, если расположена внутри его и касается всех его сторон.

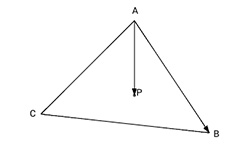
Решение некоторых задач требует иногда определить находится точка внутри треугольника или нет. Есть довольно