Расположенные на плоскости прямые (а) и (b), называются перпендикулярными, если при пересечении образуют четыре одинаковых угла, равных 90 градусам.
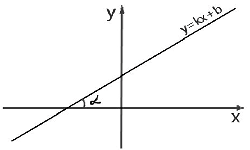
1. Прямую, проходящую через точку М1 (х1 , у1 ) и перпендикулярную к прямой у = kx + b можно представить уравнением: у — у1 = -1 / k (x — х1).
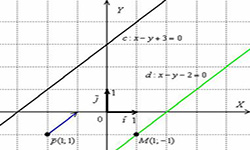
2. Прямую, проходящую через точку М1 (х1 , у1) и перпендикулярную к прямой Ax + By + C = 0, можно представить в виде уравнения A (y-y1) — B (x-x1) = 0.
3. Пусть дана прямая y = k1x + b1, тогда уравнение перпендикулярной ей прямой (при условии перпендикулярности) будет иметь вид у = -1 / k1 x + b2.
Если прямая проходит через точку M (x0 ; y0), ее координаты удовлетворяют уравнению прямой. Подставив координаты x0 ; y0, мы найдем b.
у0 = -1 / k1 x0 + b2, отсюда b2 = у0 + 1 / k1 x0
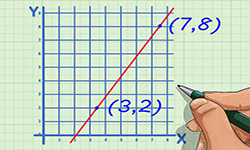
Рассчитать формулу для перпендикулярной прямой вам поможет онлайн калькулятор. Для этого следует ввести исходные параметры (х1 ; y1) (x2 ; y2) и нажать кнопку Вычислить.