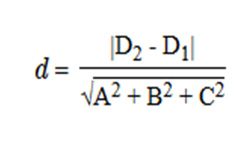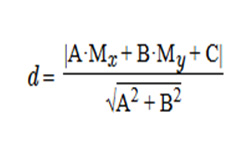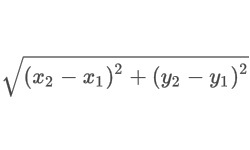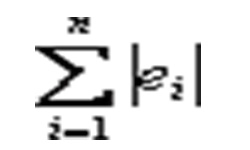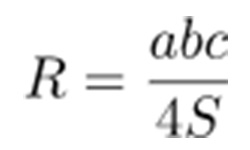При проектировании металлических, строительных и других конструкций важно уметь правильно и максимально точно вычислять расстояние между точками и плоскостями.
Возьмем точку М1 и проведем из нее перпендикуляр на заданную плоскость. Обозначим основание перпендикуляра на плоскости Н1. Длина перпендикуляра М1Н1 будет наименьшим расстоянием между точкой и плоскостью.
Если известны координаты точек М1 (х1, у1, z1) и Н1 (х2, у2, z2), расстояние от точки до плоскости, можно рассчитать по формуле для определения расстояния между точками: ![]()
Если даны координаты точки и уравнение плоскости, можно воспользоваться формулой Герона и найти расстояние между ними.
Исходя из общего уравнения плоскости Ax + By + Cz + D = 0, расстояние d от точки М с координатами (Мх, Му, Мz) до плоскости, заданной уравнением, можно рассчитать по формуле: 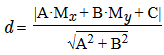 ,
,
где х, у, z — координаты точки М; А, В, С, D — коэффициенты уравнения плоскости.
Т.е. длина перпендикуляра (d) равняется модулю суммы произведений коэффициентов уравнения на соответствующие координаты точки деленному на корень квадратный из суммы квадратов коэффициентов А, В, С.
Для определения расстояния от точки до плоскости вы можете воспользоваться онлайн калькулятором.
- введите координаты точки;
- введите коэффициенты для уравнения плоскости;
- нажмите Вычислить.