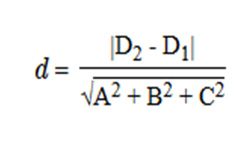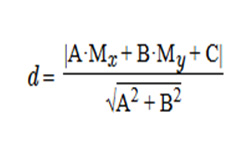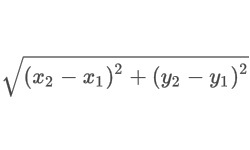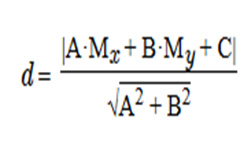Если треугольник вписан в окружность так, что его вершины располагаются на окружности, такая окружность называется описанной, а треугольник считается вписанным в данную окружность.
Центр окружности расположен в точке пересечения серединных перпендикуляров, проведенных к сторонам треугольника. Серединный перпендикуляр — прямая, которая проходит через середину отрезка, перпендикулярно ему.
Вокруг треугольника возможно описать только одну окружность.
Чтобы определить радиус R описанной окружности, необходимо произведение сторон треугольника (a × b × с) разделить на учетверенную S — площадь треугольника:
R = (a × b × с) / 4S.
Если окружность описана около равностороннего треугольника, радиус R равняется:
R = a /√3.
В том случае, когда окружность описана около прямоугольного треугольника, середина его гипотенузы (с ) является центром описанной окружности.
Радиус R составляет ½ гипотенузы: R = с/2.
Радиус окружности R также равняется медиане m, проведенной к гипотенузе: R = m.
Воспользовавшись онлайн калькулятором, вы сможете быстро и правильно определить координаты центра описанной окружности.