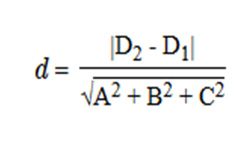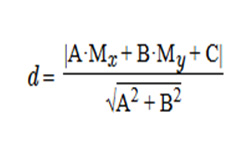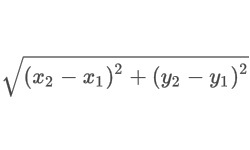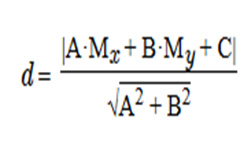Центр и радиус вписанной окружности в треугольник

Окружность считается вписанной в треугольник, если расположена внутри его и касается всех его сторон. Треугольник называют описанным около окружности. Центр вписанной окружности расположен в точке пересечения биссектрис углов этого треугольника, он равноудален от всех его сторон. В любой треугольник можно вписать только одну окружность.

Радиус r окружности, вписанной в треугольник, равняется:
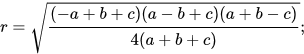где а, b, с — стороны треугольника.

Радиус вписанной окружности можно рассчитать по формуле:
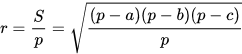, где S — площадь треугольника; р — полупериметр треугольника, равный (а + b + с) / 2.

Радиус окружности r, вписанной в равносторонний треугольник равняется:
, где а — сторона.

Радиус окружности r, вписанной в прямоугольный треугольник, равняется:

, где а, b, с — стороны треугольника

Если треугольник равнобедренный и известны стороны, радиус вписанной в него окружности r можно рассчитать по формуле:
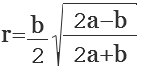, где а — сторона, b — основание.

Если известна сторона равнобедренного треугольника и угол, радиус вписанной окружности r рассчитываем по формуле:

r = a·sin a·cos a/ 1 + cos a

Чтобы быстро рассчитать центр и радиус вписанной окружности, воспользуйтесь онлайн калькулятором. Чтобы выполнить расчет:

• введите в поле калькулятора заданные величины;
• нажмите Вычислить. В считанные секунды калькулятор рассчитает центр вписанной окружности и радиус.