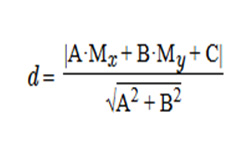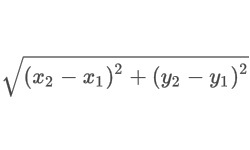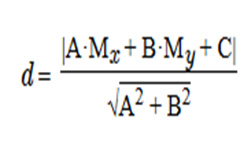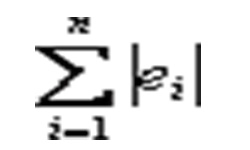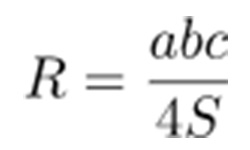Расстояние между параллельными плоскостями равняется величине перпендикуляра, проведенного из точки, принадлежащей одной плоскости, на другую плоскость. Точку берем произвольно, т.к. все точки одной плоскости, расположены на равном расстоянии от другой, параллельной первой плоскости.
Из точки А, взятой на плоскости а, опустим перпендикуляр на параллельную ей плоскость b. Обозначим основание перпендикуляра М. Величина отрезка [AM] и будет кратчайшим расстоянием между данными плоскостями.
Если параллельные плоскости представлены уравнениями, расстояние между ними можно определить методом координат.
Пусть даны 2 параллельные плоскости в системе координат Охуz.
1-й плоскости соответствует общее уравнение плоскости Ax + By + Cz + D1 = 0,
2-й плоскости — уравнение вида Ax + By + Cz + D2 = 0.
Уравниваем в обоих уравнениях плоскостей коэффициенты при переменных х,у,z (кроме свободного члена D).
После чего определяем расстояние между плоскостями (d), воспользовавшись формулой: 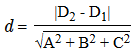
Свободный коэффициент в 1-м уравнении — D1, во 2-м — D2.
Т.е. расстояние между плоскостями рассчитывается как отношение модуля разности свободных коэффициентов |D2 — D1| к корню квадратному из суммы квадратов коэффициентов А, В, С.
Для расчета расстояния между плоскостями можно воспользоваться онлайн калькулятором.
- введите данные в уравнение 1-й плоскости;
- введите данные в уравнение 2-й плоскости;
- нажмите кнопку Вычислить.