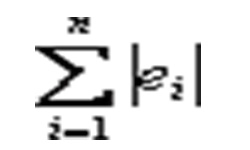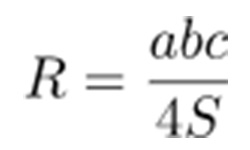Перпендикуляр, проведенный из любой вершины треугольника на противолежащую ей сторону, будет его высотой, а сторона — основанием. Если из каждой вершины треугольника провести высоту, то точка пересечения этих высот (с возможным их продлением) является ортоцентром треугольника, как правило, обозначается Н.
Высоту треугольника (h), опущенную на сторону а можно определить через сторону и угол: ha = csinβ = bsinγ, где а — основание треугольника, b, с — стороны, β, γ — углы прилежащие к основанию.
Также длину высоты можно вычислить через радиус описанной окружности R и стороны (b, с) / h = (b · с) / 2R.
Исходя из вида треугольника ортоцентр может располагаться:
- внутри треугольника (в случаях с остроугольными треугольниками);
- за его пределами (в тупоугольных треугольниках, где один угол больше 90);
- совпадать с вершиной прямого угла, если треугольник прямоугольный.
Ортоцентр треугольника и любая из его вершин будут ортоцентром треугольника, вершины которого находятся в остальных трех точках. Эти четыре точки считаются ортоцентрической системой точек. У окружностей, проведенных через 3 точки данной системы, радиусы равны.
Ортоцентр остроугольного тр-ка служит центром вписанной в его ортотреугольник окружности.
Центр описанной около треугольника окружности является ортоцентром треугольника, вершины которого расположены в серединах сторон данного тр-ка.
На прямой Эйлера располагается центр описанной окружности, центроид и ортоцентр треугольника.
Отрезок от вершины до ортоцентра (Н) в 2 раза больше отрезка от центра описанной окружности (О) до стороны, противоположной вершине.
Сумма квадратов отрезка от вершины до ортоцентра и стороны, расположенной против этой вершины, равняется учетверенному квадрату радиуса описанной окружности ®.
Пусть отрезок АН соединяет вершину А треугольника АВС с ортоцентром Н, а сторона а противолежит этой вершине, тогда: АН2 + а2 = 4 R2.
С помощью калькулятора можно быстро вычислить ортоцентр треугольника.