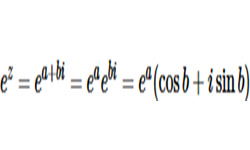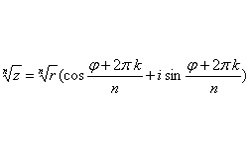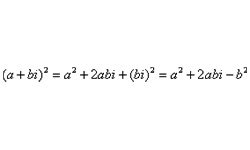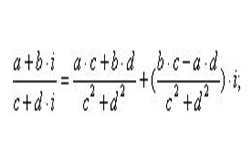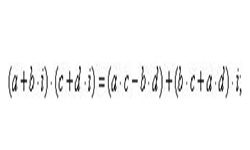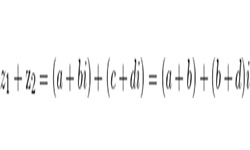Комплексными называются двумерные числа вида z = а + bi, состоящие из действительной и мнимой части. В них a, b — действительные числа, i — мнимая единица при возведении которой в квадрат получается «–1».
С комплексными числами можно производить такие же алгебраические действия, как и с действительными числами (сложение, вычитание, умножение, деление).
Вычитание комплексных чисел выполняется по тем же правилам, что и вычитание действительных чисел. При вычитании комплексных чисел получается комплексное число, действительная часть которого равняется разности действительных частей, а мнимая часть — разности мнимых частей чисел z1 и z2.
Пусть даны два комплексных числа : z1 = а + bi и z2 = с + di.
Разностью этих чисел будет комплексное число вида: z1 — z2 = а — с + i (b — d).
При решении задач следует учесть, что вычитаемое нужно вначале взять в скобки, а потом скобки раскрыть, заменив знаки.
Например,
z1 = -4 + 3i, z2 = -5 + 5i
z1 — z2 = -4 + 3i — (-5 + 5i) = -4 + 3i + 5 — 5i = 1 — 2i
С помощью онлайн калькулятора вы сможете быстро выполнить вычитание комплексных чисел. Вам необходимо лишь ввести значения в соответствующие окна калькулятора и нажать кнопку.
Комплексные числа
| + i * | + i * | ||||
| Количество знаков после разделителя дроби в числах: | |||||