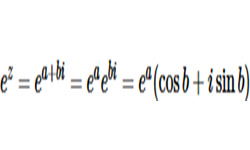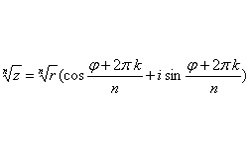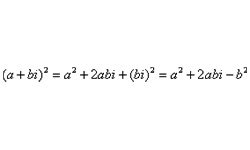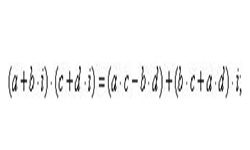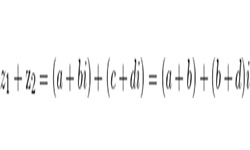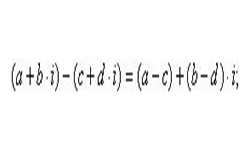Число, состоящее из вещественной и мнимой частей вида z = а + bi, является комплексным числом. Такие операции, как сложение и вычитание, умножение и деление двух комплексных чисел выполняются так же, как и соответствующие операции над действительными числами.
Деление выполняется для чисел, представленных в любой форме записи.
Деление комплексных чисел представляет собой операцию, обратную умножению. Вначале операцию деления надо записать в виде дроби, затем числитель и знаменатель умножить на выражение, сопряженное знаменателю.
Пусть даны два комплексных числа z1 = а + bi и z2 = с + di.
Деление этих чисел в алгебраической форме можно выразить формулой: 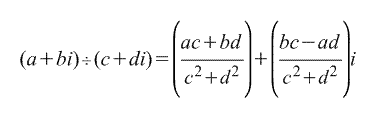
Деление в тригонометрической форме.
Пусть заданы 2 комплексных числа: ![]() ,
, ![]() , r2 — не равно 0.
, r2 — не равно 0.
Модуль числа z обычно обозначается |z| или r. В нашем случае r1 — модуль числа z1, r2 — модуль z2.
Частное от деления рассчитаем по формуле: 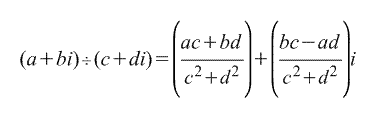
Т.е. чтобы найти частное от деления комплексных чисел, следует разделить их модули (r1 / r2) и определить разность аргументов делимого и делителя.
Комплексные числа
| + i * | + i * | ||||
| Количество знаков после разделителя дроби в числах: | |||||