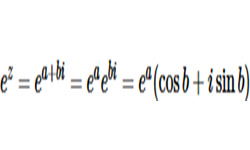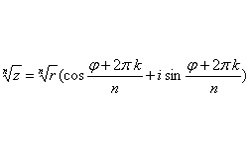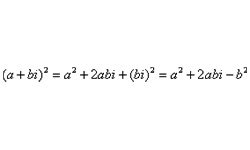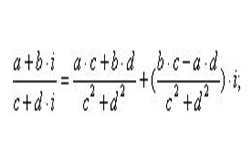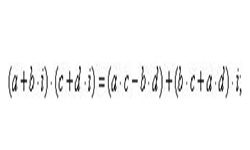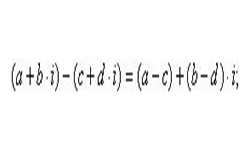Комплексное число — двумерное число вида z = а + bi, в котором выражение (а + bi) обозначает единое число, а не сумму чисел, a, b — действительные числа; i — мнимая единица, квадрат этого числа равен -1.
Число а в комплексном числе z называется действительной частью (Re z), число b — мнимой частью (Im z). Формула всякого комплексного числа z включает: действительную и мнимую части. Комплексное число можно представить в алгебраической, показательной и тригонометрической форме.
Действия над комплексными числами осуществляются по тем же правилам, что и над многочленами, i в квадрате заменяют на -1.
Сложение комплексных чисел выполняется как и сложение действительных чисел.
Пусть даны 2 комплексных числа: z1 = а + bi и z2 = с + di, которые нужно сложить. Для этого необходимо просуммировать их действительные части и просуммировать их мнимые части, при этом, от перестановки мест слагаемых сумма не изменится: z1 + z2 = z2 + z1.
Результатом сложения двух заданных чисел будет комплексное число вида: z1 + z2 = (а + с) + i (b + d).
С помощью онлайн калькулятора можно легко производить сложение комплексных чисел.
| Первое число: | Второе число: | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
+ |
|
= |