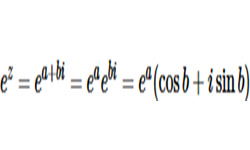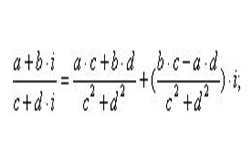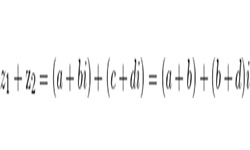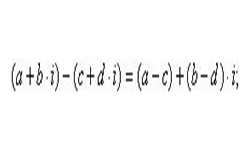Умножение комплексных чисел происходит по правилам умножения многочленов.
Пусть даны два комплексных числа: z1 = а + bi и z2 = с + di.
Произведением этих чисел будет комплексное число вида: z1z2 = (ac — bd) + i (ad + cb).
Если числа представлены в тригонометрической форме: z1 = |z1|• (соs ф1 + isin ф1),
z2 = |z2|• (соs ф2 + isin ф2), то при умножении следует перемножить их модули, а аргументы сложить: z1z2 = |z1|•|z2|• (соs (ф1+ф2) + isin (ф1+ф2)).
|z1|,|z2| — модули комплексных чисел z1, z2; ф1, ф2 — их аргументы.
Несложно выполнить операцию умножения с комплексными числами, представленными в показательной форме.
Пусть комплексное число z1 = |z1|eiф1 нужно умножить на z2 =|z2|eiф2, тогда:
z1⋅z2 = |z1|eiϕ1⋅|z2|eiϕ2 = |z1|⋅|z2|eiϕ1+iϕ2 = |z1|⋅|z2|ei (ϕ1+ϕ2)
Отсюда, при умножении двух комплексных чисел их модули перемножаются, а аргументы складываются.
Быстро найти произведение комплексных чисел можно с помощью онлайн калькулятора. Для этого необходимо ввести исходные значения в соответствующие окна калькулятора, нажать кнопку умножения.
Комплексные числа
| + i * | + i * | ||||
| Количество знаков после разделителя дроби в числах: | |||||