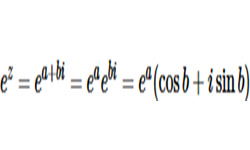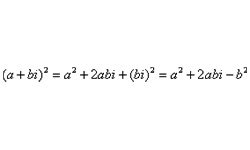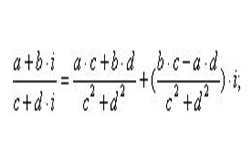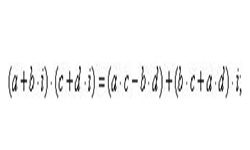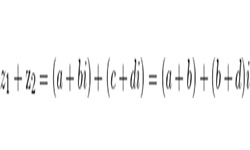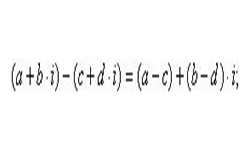Двумерные числа вида z = а + bi называются комплексными числами. Выражение (а + bi) является единым числом, в котором а, b — действительные числа, i называется мнимой единицей, возведение которой в квадрат дает отрицательный результат «–1».
Корнем n-ой степени из комплексного числа z считается комплексное число w, n-я степень которого равна z, обозначается 
Корень n-ой степени из комплексного числа имеет n разных значений.
Если число z представлено в тригонометрической форме: z = |z|• (соs ф + isin ф), то все значения корня n-ой степени находятся по формуле, выведенной английским математиком Муавром: 
В этой формуле: |z| — модуль комплексного числа z, ф — аргумент, k — параметр, значения которого (0,1,2,...n -1).
На комплексной плоскости все значения корня являются вершинами правильного n-угольника, вписанного в окружность радиуса 
с центром в начале координат.
Если комплексное число z, из которого нужно извлечь корень n-ой степени, представлен в алгебраической или показательной форме, необходимо вначале:
— представить число в тригонометрической форме, для чего вычислить модуль |z| и аргумент (ф);
— полученные значения подставить в тригонометрическую форму: z = |z| • (соs ф + isin ф);
— извлечь корни по приведенной ранее формуле.
| z = | + i | |
| n = | ||
| Количество знаков после разделителя дроби в числах: | ||
