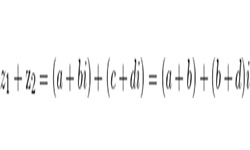Комплексное число — это двумерное число вида z = а + bi, где a, b — действительные числа; i — мнимая единица, квадрат этого числа равен -1.
Пусть показателем степени числа е является комплексное число. Согласно определения: 
Если z является действительным числом, т.е z = а = а + 0•i, тогда еz = еа.
Если z является мнимыи числом, т.е z = bi, тогда 
. Полученное равенство называется формулой Эйлера.
Любое комплексное число (за исключением 0) можно представить в показательной форме: z = |z| • еiф, где |z| — модуль, ф — аргумент комплексного числа.
Представим комплексное число в тригонометрической форме: z = |z| • (соs ф + isin ф), где согласно формулы Эйлера: соs ф + isin ф = еiф, отсюда, получим комплексное число в показательной форме: z = |z| • еiф.
С комплексными числами, представленными в показательной форме, можно довольно легко выполнять операции уиножения, деления, возведения в степень.
