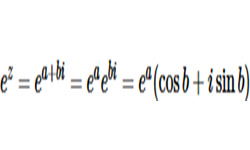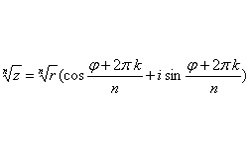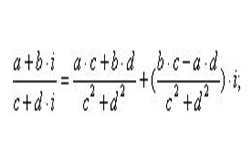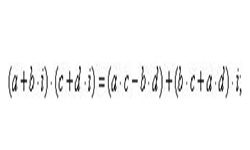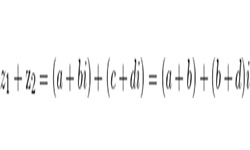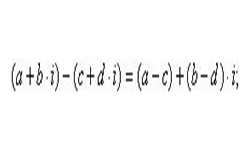Числа вида а + bi, где а и b — действительные числа, а i — число особого рода, квадрат которого равен «–1», называются комплексными числами.
Чтобы возвести комплексное число в квадрат, можно воспользоваться формулой сокращенного умножения: ![]() , где i в квадрате заменяют на -1.
, где i в квадрате заменяют на -1.
Чтобы возвести комплексное число в 6-ю, 10-ю или другую степень используют тригонометрическую форму комплексного числа и формулу Муавра: (соs ф + isin ф) в n-ой степени = соs (nф) + isin (nф).
Если комплексное число, представленное в тригонометрической форме: ![]() возвести в натуральную степень n, получим:
возвести в натуральную степень n, получим: ![]()
Формула получена согласно правил умножения комплексных чисел: ![]() .
.
Для возведения числа z в целую степень n, представим его в показательной форме: z = |z|•еiф, после чего возведем модуль в степень, а аргумент увеличиваем в n раз ![]() .
.
Если комплексные числа представлены в показательной форме: z1 = |z1| • е iф1, z2 = |z2| • еiф2, то формула возведения в степень будет иметь вид: ![]()
С помощью онлайн калькулятора можно быстро возводить комплексные числа в степень.
| z = | + i | ||
| n = | |||
| Количество знаков после разделителя дроби в числах: | |||