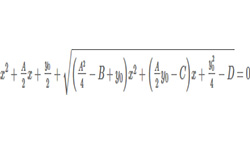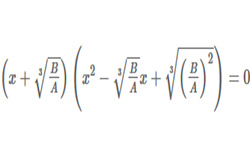Уравнение третьей степени

Часто при решении математических, статистических, инженерных задач приходится решать разные уравнения.

Уравнение 3-й степени — это кубическое уравнение вида ax³ + bx² + cx + d = 0, где а не равно 0. Число х считается корнем уравнения, если при его подстановке получается верное равенство.

Для графического анализа уравнения используется кубическая парабола.

Имеются разные способы решения кубических уравнений, среди них: теорема Безу, формулы Кардано, Виета, метод возвратного уравнения.

Кубические уравнения вида: х³ = а имеют корень x = ³√a

В некоторых случаях при решении уравнений:

• в левой части уравнения можно сгруппировать слагаемые;
• разложить ее на множители;
• найти корни.

Решение уравнения методом Кардано начинается с приведения исходного кубического уравнения ax³ + bx² + cx + d = 0 к более простому виду: y³ + py + q = 0, если заменить х неизвестным у при условии х = у — b / 3а.

В данном уравнении:
Кубическое уравнение имеет 3 корня, разберем их с помощью дискриминанта:

Δ = — 4b³d + b²c² — 4ac³ + 18abcd — 27a²d²

• если дискриминант больше 0, уравнение имеет 3 вещественных корня;
• если меньше 0, 1 — вещественный корень и 2 комплексных;
• если меньше 0, тогда хотя бы 2 корня совпадают.

С помощью онлайн калькулятора можно намного быстрее решить кубическое уравнение, найти его корни.