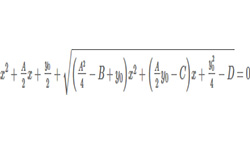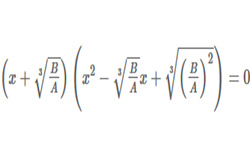Помощник в обучении Сайт помощник в обучении. Онлайн калькуляторы, тренажеры и справочники для решения и выполнения математических и других видов задач
Равенство с неизвестными числами, которые нужно найти, называется уравнением. Обозначаются неизвестные чаще всего буквами х, у, z. Решить уравнение — это определить все его корни, которые являются значениями неизвестных, при которых уравнение становится числовым равенством. Уравнения, имеющие одинаковые корни, считаются равносильными.
Чаще всего в математической практике нужно решать квадратные уравнения. Уравнения вида: ах2 + bх + с = 0 называются квадратными. Здесь коэффициенты а, b и свободный член с являются числами, при этом, а не равняется 0; х — переменная.
Квадратные уравнения бывают полными и неполными.
Если а, b, с не равны 0, уравнение называется полным.
Если b и с равны 0, уравнение будет неполным и примет вид: ах2 = 0, у данного уравнения единственный корень х = 0.
Другие случаи неполного уравнения: ах2 + с = 0 при b = 0; ах2 + bх = 0 при с = 0.
Уравнение, в котором а = 1, называется приведенным. Такое уравнение имеет вид: х2 + bх + с = 0.
Для решения таких уравнений применяют теорему Виета, согласно которой: сумма корней приведенного квадратного уравнения х2 + bх + с = 0 равняется — b, а произведение корней равняется свободному члену с, т.е. х1 + х2 = — b, х1 • х2 = с.
Быстро решать уравнение самых разных типов: линейные, нелинейные, алгебраические, полиномиальные и т.д. вы можете с помощью онлайн калькулятора.
