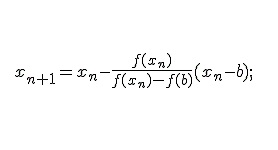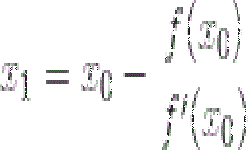На практике очень часто приходится решать задачи, связанные с решением нелинейных уравнений. Дихотомия или метод деления пополам — наиболее простой и надежный метод вычисления корней уравнения f (х) = 0, основанный на пошаговом сужении промежутка, в котором находится единственный корень уравнения, пока не добиться заданной точности.
Возьмем две точки х0 и х1, в которых значения функции f (х0) и f (х1) имеют разные знаки. В этом случае между ними имеется хоть один корень функции f.
Разделим промежуток между точками х0 и х1 пополам, обозначим середину отрезка точкой х2, которая равняется: х2 = (х0 + х1) / 2. Тогда f (х2) f (х0) <= 0 или f (х1) f (х0)<= 0.
Выбираем ту часть отрезка, на концах которого функция имеет разные знаки, и вновь делим полученный отрезок пополам. С каждым делением точность увеличивается вдвое. Деление «разнознакового» отрезка продолжаем, пока не сузится область нахождения корня функции, что поможет наконец найти его с большой степенью точности. Деление обычно проводят, пока длина отрезка становится меньше удвоенной точности вычислений. Середина последнего отрезка с разными знаками на концах будет приближенным значением корня.
Быстро решить нелинейное уравнение методом дихотомии можно с помощью онлайн калькулятора. Вам нужно: ввести интервал, указать точность вычислений.
| a = | b = |
| Введите точность: | ε = | |
| Введите левую часть уравнения (неизвестная — x): |
f (x) = | |
| Количество знаков после разделителя дроби в числах: | ||
|
|
||