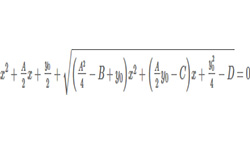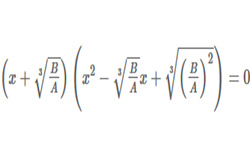Уравнение ах + b = 0, в котором есть лишь одна переменная (х) и только в 1-й степени, называется линейным уравнением с одной переменной.
Значение переменной, при которой линейное уравнение становится равенством, является корнем уравнения. Корнем может быть только число, принадлежащее области определения уравнения. Решить уравнение — это найти корни уравнения или установить их отсутствие.
Находим корень уравнения:
— переносим слагаемые с переменной в одну сторону, без переменной в другую ах = -b;
— разделим уравнение на коэффициент (а) при переменной х = -b/а.
Т.к. при переносе слагаемого с противоположным знаком в другую часть уравнение получается с теми же корнями, то х = b/а, где коэффициенты а, b — действительные числа, х — переменная.
- если а не равно 0, b — любое значение, уравнение имеет 1 корень;
- если а и b равны 0, решений бесконечное множество;
- если а равно 0, b — не равно, уравнение не имеет корней.
Уравнение вида ах + by + с = 0, в котором аргументы представлены только в первой степени, является линейным уравнением с двумя переменными. Графиком такого уравнения является прямая линия, отсюда его название — линейное.
Коэффициенты а, b, с — действительные числа (а и b не равны 0), х, у — переменные.
Любая пара чисел (х,у), которая превращает уравнение с переменными ах + by + с = 0 в числовое равенство, является решением уравнения.
Уравнения, имеющие одинаковые решения, считаются равносильными.
Уравнения, не имеющие решений, тоже равносильные.
Уравнение считается равносильным исходному, если из одной его части перенести слагаемое в другую часть, поменяв знак.
Если обе части уравнения умножить или разделить на одно и то же число (кроме 0), получим уравнение, равносильное первоначальному.
Уравнение ах + by + с = 0 можно преобразовать в уравнение вида:
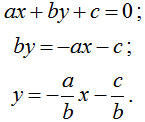
Далее коэффициентом k обозначим - ![]()
коэффициентом m - ![]() получаем уравнение у = kх + m
получаем уравнение у = kх + m
Чтобы быстро и правильно решить линейное уравнение, воспользуйтесь онлайн калькулятором.