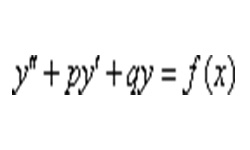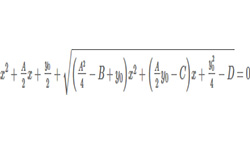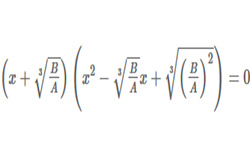При решении многих задач в математике, физике, электротехнике часто возникает необходимость в решении уравнений с комплексными корнями, извлечении корней из комплексных чисел.
Пусть дано комплексное число z, из которого надо извлечь корень n. Для этого находим модуль |z| и аргумент (ф) комплексного числа.
Корень числа находим по формуле: ![]()
Результатом решения квадратных уравнений вида ах2 + by + с = 0 с комплексными коэффициентами являются комплексные корни 2-го порядка.
Для решения квадратного трехчлена необходимо вычислить дискриминант (D):
D = b2 — 4ac, затем найти корни, которые зависят от знака D. Квадратное уравнение имеет 2 корня.
- если D больше 0, уравнение имеет 2 вещественных корня;
- при D = 0 у уравнения 1 корень х = -b / 2а;
- при D меньше 0 — 2 мнимых корня (вещественных корней нет).
Общая формула: 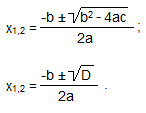
Любое уравнение вида ![]() имеет п комплексных корней. Часть из них, возможно и все, — действительные.
имеет п комплексных корней. Часть из них, возможно и все, — действительные.
Существует универсальный способ извлечения корней из любого комплексного числа.
Пусть дано уравнение ![]() , где w — комплексное число. Найти все n корней уравнения (z0, z1, z2, ...z n-1) можно по формуле:
, где w — комплексное число. Найти все n корней уравнения (z0, z1, z2, ...z n-1) можно по формуле: ![]()
|w| — модуль комплексного числа w, ф — его аргумент, k = 0, 1, 2, ...n-1
С помощью онлайн калькулятора вы сможете быстро вычислять комплексные корни заданного многочлена.