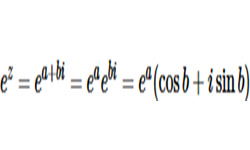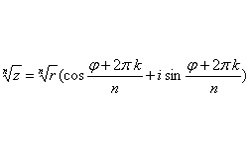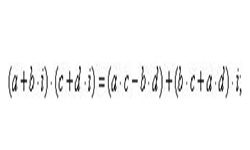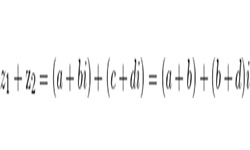Аргумент и модуль комплексного числа

Всякое комплексное число (за исключением 0) z = а + bi можно выразить в тригонометрической форме: , где |z| — модуль комплексного числа z, часто обозначается как p или r.

Модуль — это длина радиус-вектора от начала координат (0,0) до заданной точки на комплексной плоскости (а,b). Эта величина всегда неотрицательна. Формулу модуля можно вывести из теоремы Пифагора: , где а, b могут принимать любые значения.

Аргумент комплексного числа (аrg z) — величина угла ф, расположенного между положительным направлением оси Ох и радиус-вектором, проведенным от начала координат (0,0) к заданной точке (а,b). Его обозначают как ф или аrg z.

Для z = 0 аргумента нет.

Для z, расположенного в правой полуплоскости (а больше 0) аrg z = аrсtg b/а;

При а меньше 0, b больше 0 (2-я координатная четверть) аrg z = π + аrсtg b/а;

При а и b меньше 0 (3-я координатная четверть) аrg z = — π + аrсtg b/а.

Из тригонометрической формы записи получаем такие формулы:

1. |z1z2| = |z₁|• |z₂|;

2. аrg (z₁z₂) = аrg z₁ + аrg z₂;

3. 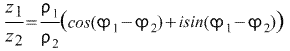, где p — модуль комплексного числа

4. . Из формула Муавра получается формула корня n-й степени из комплексного числа: 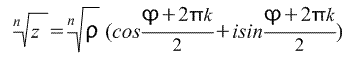, где p — модуль комплексного числа; k = 0,1,2,...n-1.