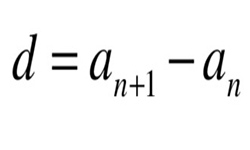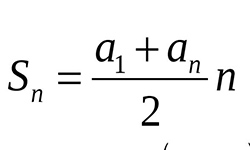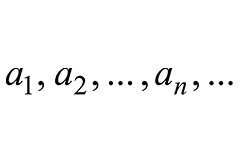Прогрессия представляет собой последовательную совокупность величин, где соблюдается зависимость каждого последующего значения от предыдущего. Каждый последующий член геометрической прогрессии, начиная со второго, равняется предыдущему, умноженному на постоянное для этой последовательности число (знаменатель), кроме нуля.
Геометрическая прогрессия называется бесконечно убывающей, если знаменатель |q| < 1. Суммой бесконечно убывающей прогрессии является число, к которому неограниченно приближается сумма ее первых членов при неограниченном возрастании числа.
Рассчитать сумму членов бесконечно убывающей прогрессии можно по формуле:
Рассчитать сумму бесконечно убывающей прогрессии вам поможет онлайн калькулятор. Для этого вам потребуется ввести данные ее первого члена и знаменателя (q).
 Помощник в обучении Сайт помощник в обучении. Онлайн калькуляторы, тренажеры и справочники для решения и выполнения математических и других видов задач
Помощник в обучении Сайт помощник в обучении. Онлайн калькуляторы, тренажеры и справочники для решения и выполнения математических и других видов задач