Помощник в обучении Сайт помощник в обучении. Онлайн калькуляторы, тренажеры и справочники для решения и выполнения математических и других видов задач
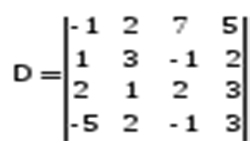
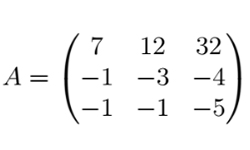Очень часто приходится размещать какие-то данные в форме таблиц. Матрица — прямоугольная таблица данных, представленных в виде чисел, взятая в круглые скобки. Размеры матрицы зависят от количества строк и столбцов. Квадратной считается матрица, имеющая одинаковое число строк и столбцов. Матрица размера n х m имеет n строк и m столбцов. Как правило, обозначают матрицы большими буквами латинского алфавита. К примеру, матрица А, ее элементы обозначаются как aij. Здесь i и j — номер строки и столбца, где стоит элемент. Строка, где элементы равны 0, называется нулевой. Строка, в которой хоть один элемент не равен нулю, называется ненулевой. Соответственно, нулевым называется столбец с элементами, равными 0, ненулевым — хоть один из элементов столбца не равен нулю.
Матрицы впервые появились в математике в процессе линейных преобразований, при решении систем линейных уравнений. При сложении двух матриц складываются соответствующие элементы этих матриц. Как сложение, так и вычитание производится только с равными матрицами. Складывая две равных матрицы (А + В), получаем матрицу с аналогичным размером ©. Элементы матрицы С равняются попарной сумме соответствующих элементов заданных матриц А и В. Элемент матрицы С можно рассчитать как сij = aij + bij. При выполнении операции вычитания матриц (А — В) получаем матрицу С, элементы которой равняются попарной разности соответствующих элементов данных матриц А и В, т.е. сij = aij — bij.
Тегиматрицы
