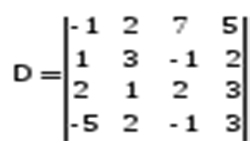
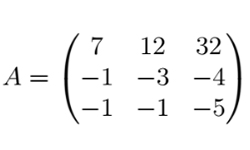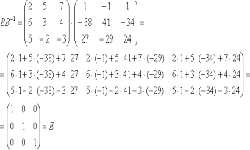В линейной алгебре очень важны понятия собственный вектор и собственное число, которые рассчитываются для квадратной матрицы или линейного преобразования. Собственный вектор — вектор, при умножении на который матрицы или в результате применяемого к нему преобразования, получаем коллинеарный вектор. Под понятием коллинеарного вектора подразумевается вектор, умноженный на некую скалярную величину, называемую собственным числом матрицы или линейного преобразования.
Ненулевой вектор Х называется собственным вектором квадратной матрицы А, если есть ненулевое число λ, при котором АХ = λ Х.
Число λ называется здесь собственным значением вектора Х относительно матрицы А.
Матрица А -λ E называется характеристической матрицей матрицы А,
уравнение |A - λ E| = 0 называется характеристическим уравнением матрицы А. Корни этого уравнения будут собственными числами матрицы А.
При решении однородной системы уравнений:
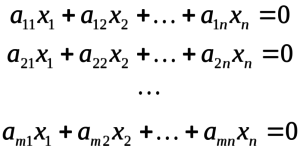
определяем вектор Х, который соответствует собственному значению λ.