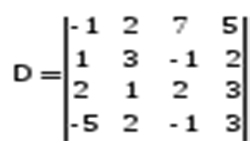
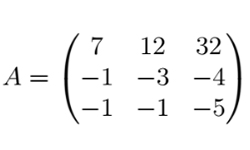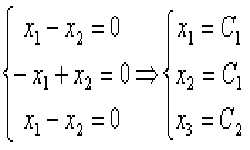В задачах, требующих экономического анализа, других прикладных задачах при решении матричных уравнений часто необходимо построить обратную матрицу. Обратной называется матрица, при умножении которой на исходную, получают единичную матрицу (Е).
A·A-1 = A-1·A = E
При этом, исходной должна быть квадратная матрица, ее определитель не должен равняться нулю. Т.е. матрица должна быть невырожденной. Имеется несколько достаточно сложных и громоздких способов получения обратной матрицы, особенно при работе с матрицами высокого порядка.
Так, обратную матрицу можно вычислить с помощью присоединенной матрицы. Для этого к квадратной матрице справа следует приписать единичную матрицу одинакового порядка. Путем элементарных преобразований над строками преобразовываем полученную матрицу, чтобы начальная матрица стала единичной. В этом случае матрица, выведенная из единичной, стала обратной к исходной. Стоит отметить, что у исходной матрицы отсутствует обратная матрица, если в результате преобразований в левой части образуется нулевая строка (столбец).
Обратную матрицу можно рассчитать также с помощью союзной матрицы. Союзной называется матрица, у которой элементы равняются алгебраическим дополнениям соответствующих элементов исходной матрицы (А).
| A-1 = | 1 | ÃT |
| det (A) |