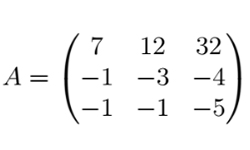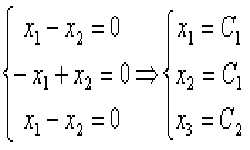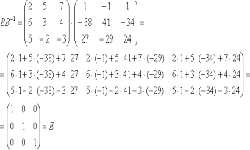Приведение матрицы к ступенчатому виду

Матрица — математический объект, представленный в форме квадратной или прямоугольной таблицы, содержащей определенное число строк и столбцов, именуемых порядками. Матрицы могут различаться размерами и содержанием. Матрицы позволяют упорядочить записи систем линейных уравнений, что ведет к удобному поиску их результатов. Работа с матрицами предполагает приведение их к стандартному виду.
В математике множество разнообразных видов матриц. Все элементы нулевой матрицы равны нулю, а число строк и столбцов может быть совершенно разным.
Матрица квадратного типа имеет одинаковое количество строк и столбцов. Матрица простейшего вида вектор-столбец имеет три численных значений, расположенных в столбец. Вектор-строка содержит три численных элементов, размещенных в одну строку. В диагональной матрице числовые значения имеют лишь элементы главной диагонали, остальные равны нулю. Начинается диагональ с элемента в правом верхнем углу и заканчивается в последнем столбце последней строки. Диагональный тип может иметь лишь квадратная матрица. Подвид диагональной матрицы — единичная, все числовые значения которой равны единицам. В канонической матрице не все компоненты основной диагонали равны единице, число строк и столбцов может быть разное, но, как и в единичной матрице, элементы, расположенные не на основной диагонали, равны нулю. Матрица треугольного типа является квадратной. Матрица, элементы которой, расположенные ниже главной диагонали, равны нулю, называется нижнетреугольной. В верхнетреугольной матрице числовые значения имеют элементы, расположенные на основной диагонали и под ней. Над диагональю элементы имеют нулевое значение.

Матрица, имеющая «ступени» из нулей, называется ступенчатой. В данном типе матриц диагональ из нулей не обязательно должна быть основной. Элементы под диагональю, как и на диагонали, должны иметь нулевые значения. Элемент в углу каждой ступеньки — ненулевой. Первый ненулевой элемент строки обязательно располагается правее первого ненулевого элемента строки предыдущей. Все элементы под 1-м ненулевым элементом строки имеют нулевые значения. Если ступенчатая матрица имеет нулевую строку, строки ниже нее тоже не имеют числовых значений. Т.е нулевые строки — последние. Для приведения матрицы к ступенчатому виду следует определить ее детерминант. Задание выполнимо, если детерминант больше или меньше нуля, в противном случае (равен нулю) привести матрицу к ступенчатому виду нельзя.

Любую матрицу несложно привести к ступенчатой форме, используя следующие элементарные преобразования:
— перестановка двух строк (столбцов);
— умножение строки (столбца) на любое, кроме нуля, число;
— сложение строки (столбца) с другой (другим), умноженной (умноженным) на любое, произвольно взятое (кроме нуля) число.

Приводим матрицу к ступенчатому виду:
1. Выбираем элемент, отличный от нуля в 1-м столбце. Если выбранный элемент (ведущий) расположен не в 1-й строке, переставляем строку с ведущим элементом на первую (ведущую) строку. Если элементы 1-го столбца равны нулю, исключаем его и переходим к следующему.
2. Делим элементы ведущей строки на ведущий элемент. Преобразования закончены при условии, что ведущая строка последняя.
3. К строке, расположенной под ведущей, добавляем ведущую, предварительно умноженную на число, чтобы элементы стоящей ниже строки стали равняться нулю.
4. Исключаем строку и столбец с ведущим элементом на пересечении.
Повторяем те же действия с оставшейся частью матрицы.

Привести матрицу к ступенчатому виду вам поможет онлайн калькулятор. Выберите размерность и введите значение ее элементов.