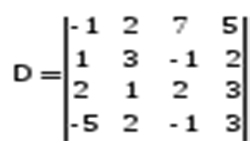
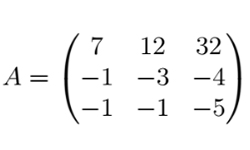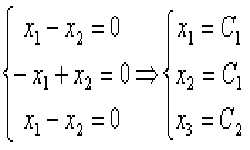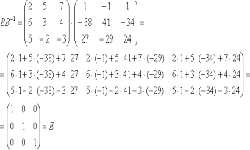Транспонированной называется матрица, полученная из исходной путем перемены местами строк и столбцов. Т.е. при транспонировании строки заданной матрицы нужно разместить в виде столбцов в том же порядке. Операция транспонирования матрицы обозначается буквой Т, которая записывается над матрицей в правом верхнем углу. Предположим, мы имеем матрицу А, состоящую из m x n элементов (m строк и n столбцов), тогда транспонированная матрица АT представляет собой набор из n x m элементов (n строк и m столбцов). Любую матрицу, независимо от количества строк и столбцов, можно транспонировать. Наиболее часто приходится производить операцию транспонирования квадратных матриц, имеющих равное количество строк и столбцов.
Свойства транспонированной матрицы:
- Матрица А, транспонированная дважды, равняется исходной матрице (А).
- Транспонированная сумма матриц равна сумме транспонированных матриц.
- Транспонированное произведение матрицы и числа равняется произведению транспонированной матрицы и числа.
- Транспонированное произведение матриц равно произведению транспонированных матриц в обратном порядке.
- Определитель исходной квадратной матрицы равен определителю транспонированной матрицы.