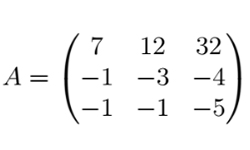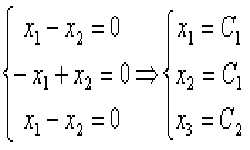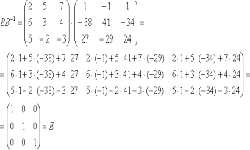Минором Δij элемента аij квадратной матрицы Аn×n (матрицы n-го порядка) будет определитель матрицы А (n-1) -го порядка, который находим способом вычеркивания i-й строки и j-го столбца из матрицы А (вычеркиваем строку и столбец, на пересечении которых расположен элемент аij).
Рассмотрим квадратную матрицу А
Пусть 
Для любого элемента аij матрицы можно найти дополнительный минор Δij посредством вычеркивания строки i и столбца j.
Алгебраическим дополнением Аij элемента аij матрицы n-го порядка является его минор, знак которого состоит из номеров строки и столбца:
Aij = (-1)i+j х Δij,
Mij — обозначение минора элемента аij.
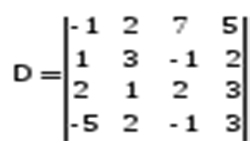
Представим матрицу 
Тогда каждому ее элементу будет соответствовать алгебраическое дополнение
(-1)i+j × Δij
Алгебраическое дополнение и минор будут одинаковыми при четной сумме номеров строки и столбца. Если сумма номеров является нечетным числом, то они будут различаться знаком.
В прямоугольных матрицах количество строк не равно количеству столбцов. В этом случае минором k-го порядка матрицы A, состоящей из m строк и n столбцов, является определитель с элементами, находящимися на пересечении k строк и k столбцов матрицы. При этом, k ≤ m и k ≤ n
С помощью онлайн калькулятора вы сможете быстро рассчитать значение минора.
| — порядок матрицы | |||||||||
| r | = | — строка | |||||||
| c | = | — столбец | |||||||
|
Mi,j
|
=
|
|
=
|
|
|
||||