Определитель матрицы

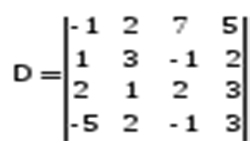
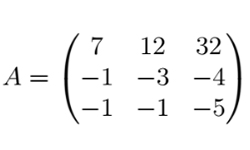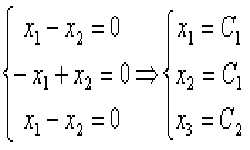При решении сложных систем уравнения большую роль играет определитель матрицы или детерминант матрицы. Это — важнейшая численная характеристика квадратной матрицы, используемая при решении многих задач. На вычислении определителя матрицы основан метод Крамера решения систем уравнений, он позволяет определять наличие и единственность решения систем уравнений. Обозначается определитель матрицы: det (A), |A|, или ∆(A). Определителем квадратной матрицы А размера n х n является число:

В данном выражении а1,а2,...,аn — перестановка чисел от 1 до n, N (а1,а2,...,аn) — количество инверсий при перестановке. Суммирование производится по всем перестановкам порядка n.

Свойства определителей:

• Определитель матрицы с двумя равными или пропорциональными строками (столбцами), с нулевой строкой (столбцом), с двумя или несколькими линейно зависимыми строками (столбцами) равняется нулю.
• Определитель единичной матрицы равняется единице: det (E) = 1.
• Определитель матрицы не меняется при транспонировании.

Способы вычисления определителя матрицы:

1. Значение определителя матрицы 1×1 равняется значению ее элемента:

3. Определитель матрицы 3×3 равен разности между суммой произведений элементов главной диагонали плюс произведение элементов лежащих на треугольниках, грань которых параллельна главной диагонали, и суммой произведений элементов побочной диагонали и элементов, лежащих на треугольниках с параллельной побочной диагонали гранью.

∆ =

a11 a12 a13 a21 a22 a23 a31 a32 a33

= a11·a22·a33 + a12·a23·a31 + a13·a21·a32 — a13·a22·a31 — a11·a23·a32 — a12·a21·a33

Значение определителя матрицы 3-го порядка (3×3) можно рассчитать, используя правило Саррюса.
4. Определитель матрицы произвольного размера рассчитывается как сумма произведений элементов строки определителя на их алгебраические дополнения.

	n
det (A) =	Σ	aij·Aij	— разложение по i-той строке
	j = 1

5. Определитель матрицы произвольного размера можно расчитать как суииу произведений элементов столбца определителя на их алгебраические дополнения:

	n
det (A) =	Σ	aij·Aij	— разложение по j-тому столбцу
	i = 1

Очень важно точно и правильно находить определитель матрицы, т.к. с увеличением размера матрицы расчеты становятся более сложными и громоздкими, что может привести к ошибке в ходе решения и окончательном ответе. С помощью онлайн калькулятора вы сможете произвести расчеты правильно и намного быстрей.

Размер матрицы: 2×23×34×45×56×67×7 Введите значения Матрицы: A =