Векторное произведение векторов

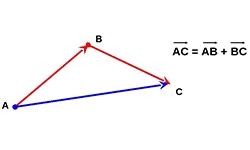
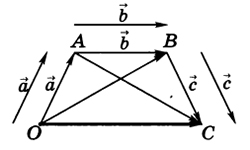
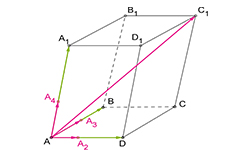
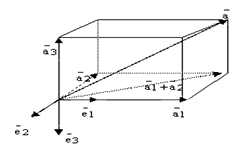
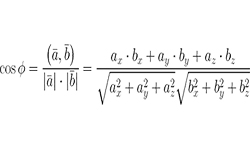Как известно, в результате скалярного произведения векторов получается число. Итогом векторного произведения векторов является вектор.

Итак, векторным произведением двух неколлинеарных векторов (а и b) называется третий вектор ©, имеющий следующие свойства:
1. длина его численно равняется площади параллелограмма, построенного на векторах а и b
2. вектор с перпендикулярный плоскости векторов а и b.
3. направление вектора с таково, что кратчайший поворот от вектора а к вектору b происходит против часовой стрелки, если посмотреть с конца вектора с.
В зависимости от направления вектора с тройка векторов а, b, с называется правой или левой. В данном случае тройка векторов а, b, с — правая.

Геометрический смысл произведения.
Модуль произведения двух векторов равняется площади параллелограмма, построенного на этих векторах:
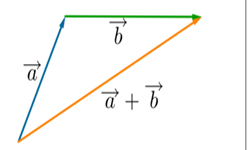
Половина модуля векторного произведения двух векторов (a и b) равняется площади треугольника, построенного на этих векторах:
Векторное произведение можно представить в координатной форме через координаты векторов а и b. Пусть а = {а_х;а_у;a_z} и b = {b_х;b_у;b_z}, тогда произведение двух векторов можно рассчитать по формуле:
Свойства векторного произведения векторов:
Векторное произведение двух параллельных между собой не нулевых векторов равняется нулевому вектору.
Векторное произведение произвольного вектора на нулевой равняется нулевому вектору.