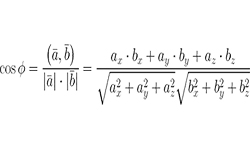Середина отрезка

Если от точки А провести прямую к точке В, то мы получим отрезок АВ, т.е отрезок — часть прямой, ограниченная с двух сторон двумя точками с определенными параметрами. Точки А и В будут концами этого отрезка. Точка, расположенная на данном отрезке и равноудаленная от обоих его концов, называется серединой отрезка. Если отрезок АВ в двухмерной системе координат имеет координаты: А (х₁;у₁); В (х₂;у₂), то координаты середины данного отрезка (точки С) можно рассчитать как сумму абсцисс (Х₁+Х₂) и ординат (Y₁+Y₂), каждую из которых нужно разделить пополам. Середина отрезка АВ (точка С) будет иметь координаты {(Х₁+Х₂)/2,(Y₁+Y₂)/2}.

Чтобы найти координаты середины отрезка АВ, расположенного в трехмерном пространстве, введем дополнительно координаты оси Z.
Пусть в прямоугольной системе координат O_xyz отрезок АВ имеет координаты A (x_a, y_a, z_a) и B (x_b, y_b, z_b), тогда координаты середины отрезка — точки С в пространстве рассчитываем по координатам его концов:

х_C = (х_A+х_B) / 2, y_C = (у_A+у_B)/2, z_C = (z_A + z_B)/2

или

С ( (х_A+х_B) / 2; (у_A+у_B)/2; (z_A + z_B)/2)

Рассчитать середину отрезка можно с помощью онлайн-калькулятора. Для этого вводим данные точек Х,Y,Z для трехмерного пространства; Х, Y — для отрезка на плоскости.