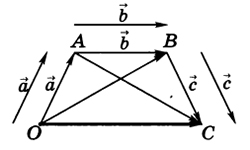
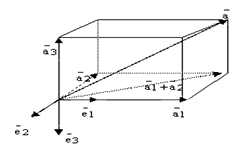
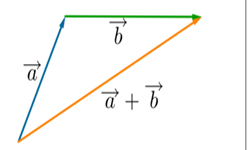
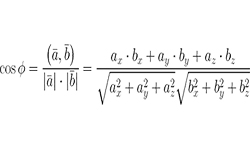Векторы, которые лежат на одной плоскости или параллельные одной плоскости, называются компланарными. Также верно и следующее определение: если три вектора, приведенные к общему началу, лежат в одной плоскости, они являются компланарными. Два вектора всегда компланарны, т.к. всегда можно найти плоскость, параллельную им.
1. Три вектора компланарны, если два из них коллинеарны.
2. В случае, когда векторы а и b не коллинеарны, но для вектора с есть единственная пара чисел x и у, когда с = х×а + у×b, то векторы а, b, с компланарны.
Отсюда: если три вектора а,b,с компланарны, а векторы а и b не являются коллинеарными, вектор с раскладывается по векторам а и b только единственным образом.
Условия компланарности для векторов:
Если смешанное произведение трех векторов равно нулю, они компланарны.
Если три вектора являются линейно зависимыми, они компланарны.
Если среди n векторов имеется не больше двух линейно независимых, вектора компланарны.
Проверить компланарность трех векторов вам поможет онлайн калькулятор.
Введите координаты векторов:
| a | = | ( | , | , | ) | |
| b | = | ( | , | , | ) | |
| c | = | ( | , | , | ) | |
|
Векторы копланарны.
Векторы не копланарны. |
||||||