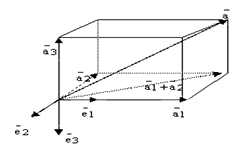
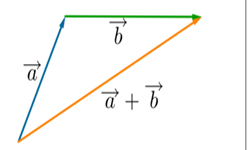
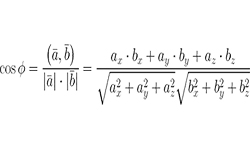Осью является прямая с указанным направлением. На направленной прямой возможно построить проекцию вектора. Проекцией вектора на ось в геометрическом понимании является вектор, в алгебраическом — число. Для построения проекции ненулевого вектора АВ на ось L на плоскости или в трехмерном пространстве необходимо из точек А и В (начала и конца вектора) опустить перпендикуляры на ось L. В результате получаем искомую проекцию 
, началом и концом которой являются основания опущенных перпендикуляров. Отсюда, геометрической проекцией вектора на ось считается вектор, началом и концом которого являются проекции начала и конца заданного вектора. Проекция вектора АВ на ось L — скалярная величина, представляющая число, равное длине геометрической проекции вектора. Записывается со знаком «+», если направление геометрической проекции совпадает с направлением оси, со знаком «-», если направления противоположны. Пусть направление оси L определяется вектором b, тогда числовую проекцию вектора а (или вектора АВ) на эту ось можно обозначить как 
Вычисляем числовую проекцию вектора на ось путем умножения длины данного вектора (а) на соs (косинус) угла между вектором а и вектором b, определяющим направление оси:
В результате преобразований формула приобретает вид:
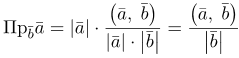Т.е. числовая проекция вектора а на ось L, направление которой совпадает с направлением вектора b, равняется отношению скалярного произведения векторов (а и b) к модулю вектора b.
Проекция вектора 
на ось l равняется проекции на эту же ось вектора a, умноженного на число m
Проекции одинаковых по величине векторов на одну и ту же ось равны.
Для нахождения проекции вектора на ось воспользуйтесь онлайн калькулятором. Вам необходимо лишь ввести координаты вектора (две, если вектор задан на плоскости, три, если в пространстве).
