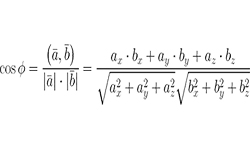Скалярное произведение вектора а на векторное произведение вектора b и вектора считается смешанным произведением векторов и равняется определителю матрицы, составленной из этих векторов.
Для нахождения смешанного произведения векторов, заданных координатами a = {ax; ay; az}, b = {bx; by; bz} и c = {cx; cy; cz}, воспользуемся формулой:
| a · [b × c] = | ax | ay | az |
| bx | by | bz | |
| cx | cy | cz |
Если смешанное произведение трех не нулевых векторов будет равняться нулю, вектора — компланарные.
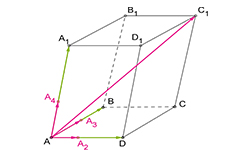
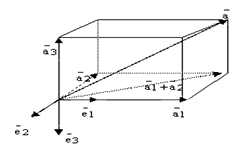
Модуль смешанного произведения трех векторов (а,b,с) равняется объему образованного ими параллелепипеда
Vпарал = |a · [b х c]|
Объем пирамиды, образованной векторами а,b,с равняется одной шестой от модуля смешанного произведения этих векторов.
Vпир = 1/6 |a · [b х c]|
Воспользовавшись онлайн-калькулятором, вы сможете быстро и правильно рассчитать смешанное произведение векторов.